16/11/2010
Eziquiel Menta
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Álgebra |
O que o aluno poderá aprender com esta aula
§ Representar graficamente uma função quadrática.
§ Comparar a função quadrática ao gráfico de uma parábola.
§ Identificar os zeros ou raízes da função quadrática.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Conhecimentos de matemática básica.
Estratégias e recursos da aula
Atividade 1
Em grupo (3 ou 4 alunos) propor aos alunos a realização da pesquisa buscando aproximações entre a Matemática e o Futebol. Para orientar essa pesquisa, o professor pode construir uma WebQuest. A WebQuest é uma metodologia de pesquisa online, organizada por meio de um roteiro que segue com os seguintes passos: introdução, tarefa, recursos, processo, avaliação, conclusão. O professor dá indicativos de sítios, pré-selecionados, para que a aula seja aproveitada ao máximo, e os alunos não se distraiam diante de tantas informações da internet, e organizem a tarefa e a concluam com sucesso. Para desenvolver sua WebQuest, o professor pode seguir as orientações do "Tutorial para criar e editar webquest", disponível em: http://rosangelamentapde.pbworks.com/f/tutorial_wq_escolabr1.pdf e, utilizar o sítio http://www.webquestbrasil.org para criar e postar. Professor, procure destacar que a ênfase da pesquisa é em buscar funções matemáticas, seja presente no tamanho e formato do campo e da bola, movimento, posição e aceleração da bola ou dos jogadores, além de demais descobertas.
Sugestão de sítios para pesquisa:
Bola de Futebol. Disponível em: http://www.dm.ufscar.br/hp/hp153/hp153001/hp153001.html, acesso em 12 de outubro de 2010.
Campo de Futebol. Disponível em: http://www.inmetro.gov.br/consumidor/produtos/campo_de_futebol.asp, acesso em 12 de outubro de 2010.
Matemática e o Futebol. Disponível em: http://www.universia.com.br/universitario/materia.jsp?materia=5620, acesso em 12 de outubro de 2010.
A Matemática do Futebol. Disponível em: http://revistaescola.abril.com.br/matematica/pratica-pedagogica/matematica-parte-reportagem-capa-copa-mundo-427101.shtml, acesso em 12 de outubro de 2010.
A bola de futebol e a Matemática. Disponível em: http://anagraziele.com/curiosidades/103-a-bola-de-futebol-e-a-matematica.html, acesso em 12 de outubro de 2010.
Probabilidades – Matemática e Futebol. Disponível em: http://www.blablagol.com.br/probabilidades-matematica-e-futebol-7, acesso em 12 de outubro de 2010.
Professor, ao final das atividades da pesquisa, em sala de aula, propor uma rodada de apresentação para que os grupos socializem as aproximacões que encontraram. Possivelmente aparecerão inúmeras possibilidades. Aproveite para destacar que todas são de igual importância.
Obs. Para essa atividade de pesquisa, se possível convide o professor de Educação Física para participar, fazendo as devidas considerações no que se refere a sua disciplina.
Propor aos alunos as atividades encontradas no objeto educacional Matemática e Futebol disponível em: http://rived.mec.gov.br/atividades/matematica/o_futebol/mat1_intro.html, acesso em 12 de outubro de 2010. Este recurso apresenta várias maneiras de se fazer conexões entre a Matemática e o Futebol.
Para fechar a atividade de pesquisa, apresente aos alunos o seguinte exemplo:
Vamos supor que um goleiro coloca a bola em jogo com um chute forte. A bola sobe até um ponto máximo e começa a descer descrevendo, uma curva.
Fonte: Imagem da autora
Professor, esboce o desenho do gráfico gerado pela bola subindo e depois descendo no quadro de giz. Após, converse com os alunos que neste caso, o caminho da bola gera uma curva. Essa curva é chamada de parábola. Etimologicamente, a palavra parábola provém do grego e significa “lançar ao longe”. Explique que esse é uma modelo de aproximação entre Matemática e Futebol que usamos ao buscar o conceito de Função Quadrática.
| O físico italiano Galileu Galilei (1564 – 1642), estudou os movimentos como o desta bola e verificou que, desprezando a resistência do ar, qualquer corpo lançado no campo de gravidade da Terra se movimenta do mesmo modo. Ou seja, no lançamento do goleiro, após 1 segundo a bola percorreria cerca de 5 X 1² = 5 metros; depois de 2 segundos, percorreria cerca de 5 X 2² = 20 metros; depois de 3 segundos percorreria, 5 X 3² =45 metros; e assim sucessivamente. Como ficaria essa expressão matemática após x segundos de tempo? Neste caso, percorreria 5 X x² metros, onde 5 é aproximadamente a metade da aceleração da gravidade em metros por segundo, em cada segundo. Assim, essa expressão pode ser escrita em forma de uma função, ou seja f(x) = 5x². Galileu juntou todos estes elementos em um importante conceito matemático: função do segundo grau ou função quadrática. Fonte: http://www.diaadiaeducacao.pr.gov.br/portals/pde/arquivos/2453-6.pdf
Assim, sempre que encontrarmos uma função, na qual a variável x aparece com o expoente máximo igual a 2 ela é chamada de função de 2º. Grau, ou Função Quadrática, pois o expoente máximo da variável é “elevado ao quadrado”. |
Professor, se julgar necessário retomar com os alunos o conceito de função, propor o recurso Estudo da função do 2º grau que permite o desenvolvimento, a ampliação e a contextualização do conceito de função do 2o. grau por meio de construção e observação de gráficos em um plano cartesiano. Disponível em: http://objetoseducacionais2.mec.gov.br/handle/mec/7903, acesso em 12 de outubro de 2010.
Após o estudo do recurso. Retome com os alunos, o gráfico do lançamento da bola e da função proposta f(x) = 5x². Explique que os conceitos da resistência do ar e do lançamento do corpo no campo de gravidade são conceitos da Física, que permitem que a concavidade da parábola se apresenta dessa forma. Se possível, convide o professor de Física para participar dessa discussão, trazendo as considerações da disciplina referentes a esse tema.
Atividade 2 - Problematização
1) Em uma partida de futebol, um goleiro faz um lançamento no qual a trajetória da bola descreve uma parábola. Essa trajetória tem uma altura y (em metros) dada pela função do tempo x (em segundos) decorrido após o chute.
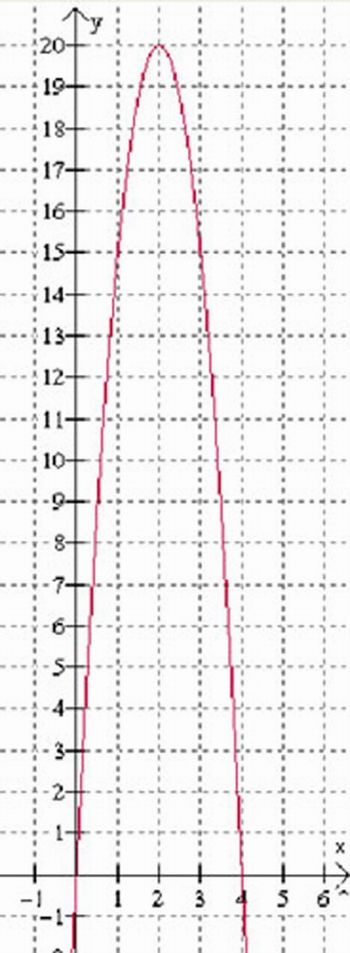
Sabendo que a trajetória da bola é dada pela função y= -5x2 + 20x, determine:
a) o gráfico da trajetória da bola no plano cartesiano.
b) determine a altura máxima da bola.
c) determine a altura da bola após 1 segundo.
Resolução:
a)
b)
Obs. Clique sobre a imagem para vê-la em tamanho maior.
c)
Sabemos que y= -5x2 + 20x, então para determinarmos no tempo de 1 segundo basta substituirmos x por 1.
y= -5. 12 + 20 . 1
y= -5 + 20
y= 15 metros
ou podemos analisar pelo gráfico quando x for igual a 1, observando sua imagem, temos y = 15.
Professor, aproveite a atividade para retomar o conceito discutido no exemplo apresentado. Aproveite também para abordar outros conceitos, como por exemplo:
a) É viável desenvolver gráfico de uma parabola com apenas 2 pontos?
b) Por que o vértice da parábola estudada teve o vértice voltado para cima? Quando uma parábola tem o vértice voltado para baixo?
c) Sabendo que as raízes da Função Quadrática são os pontos onde a parábola intercepta o eixo x. Quais as raizes da função estudada?
d) Outras questões pertinentes.
Atividade 3 - Vídeo
Em sala de aula, assistir com os alunos o vídeo Matemática no futebol [Matemática em toda parte] disponível em: http://objetoseducacionais2.mec.gov.br/handle/mec/12537, acesso em 12 de outubro de 2010.
O vídeo apresenta um episódio do programa matemática em toda parte, da TV Escola, onde são apresentados conceitos de geometria e cálculo da área de objetos a partir do futebol.
 Matemática no futebol [Matemática em toda parte]
Matemática no futebol [Matemática em toda parte]
Ao final do vídeo, solicitar aos alunos retomem dos grupos e então produzam um texto descrevendo todas as aprendizagens apreendidas a partir desta aula.
Como captar o movimento de uma bola de futebol chutada pelo goleiro? Disponível em: http://www.slideshare.net/christiansimon/objeto-de-aprendizagem-2734306, acesso em 12 de outubro de 2010.
Recursos Complementares
Anatomia de uma função quadrática, disponível em: http://www.uff.br/cdme/fqa/fqa-html/fqa-br.html, acesso em 12 de outubro de 2010.
Funções no mundo real, disponível em: http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=24797, acesso em 12 de outubro de 2010.
Vídeo “Uma parábola para Júlia” disponível em http://www.diaadia.pr.gov.br/condigital/modules/debaser/singlefile.php?id=5, acesso em 12 de outubro de 2010.
Avaliação
A avaliação deverá ser diagnóstica, processual e continua, ou seja, realizada ao longo de todas as aulas.
Critérios a serem observados:
- Desenvolvimento e realização das atividades durante a pesquisa inicial. O aluno foi participativo? Apresentou conteúdos relevantes? Demonstrou conhecimento?
- Na atividade no laboratório de informática. Participou? Raciocínio adequado?
- Participação no desenvolvimento das atividades? Foi argumentativo? Realizou as tarefas?
- Na produção textual final. Participou? Produziu? Contribuiu com o grupo?
Cinco estrelas 2 classificações
- Cinco estrelas 2/2 - 100%
- Quatro estrelas 0/2 - 0%
- Três estrelas 0/2 - 0%
- Duas estrelas 0/2 - 0%
- Uma estrela 0/2 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Elaine Bezerra de Souza, C. E. Brandão Monteiro , Rio de Janeiro - disse:
elainesouza1@yahoo.com.br11/08/2011
Cinco estrelasAdorei a sugestão e pretendo aplicá-la com a minha turma.
-
sandra rosa de faria pinto, colégio estadual gricon e silva , Goiás - disse:
srosadefaria@hotmail.com23/04/2011
Cinco estrelasEssa aula é completa, excelente.
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus






 Estudo da função do 2º grau
Estudo da função do 2º grau