12/01/2011
Mary Grace Martins
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Fundamental Final | Matemática | Espaço e forma |
O que o aluno poderá aprender com esta aula
- Conhecer conceitos de geometria espacial
- Utilizar elementos da geometria: eixos x e y
- Utilizar diferentes recursos para exploração de conceitos
- Trabalhar em grupos interagindo para atingir um objetivo comum
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
É interessante que os alunos já tenham trabalhado com noções de geometria plana e polígonos.
Estratégias e recursos da aula
O uso do computador em sala de aula pode promover a experimentação, a pesquisa e a representação do conhecimento construído. Nessa sequência de atividades, os alunos usarão uma animação para elaborar conceitos relacionados ao tema Plano Cartesiano, farão pesquisas na Internet para saber mais sobre Geometria Espacial, bem como, farão a organização de informações sobre Sólidos usando ferramentas de apresentação no computador.
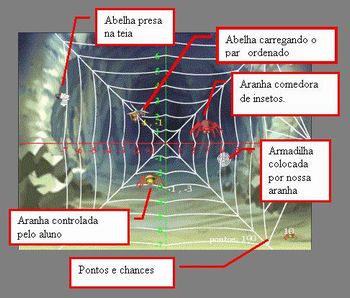
Para começar, proponha a utilização da animação  Teia Cartesiana
Teia Cartesiana
disponível no Portal do Professor em http://portaldoprofessor.mec.gov.br/storage/recursos/14694/Teia Cartesiana.exe.
Essa animação "é um jogo onde o aluno movimenta uma aranha em uma teia, que representa o plano cartesiano, com o objetivo de capturar abelhas. As abelhas apresentam as coordenadas de um ponto no plano que fazem parte do seu percurso, pela teia, e nestas coordenadas a aranha tem a possibilidade de capturar a abelha para alimentar outra aranha companheira."
Orientações sobre o Jogo Teia Cartesiana, disponível no Portal do Professor
Organize os alunos em duplas e, na sala de informática, acessem a animação. Peça que durante o jogo anotem as situações em que conseguiram marcar pontos, indicando os pares de números.
Explique que esses pares de números chamam-se Coordenadas.
Depois de explorarem o jogo, sistematize a discussão para acrescentar mais algumas informações, tais como a identificação dos eixos.
Pergunte a seus alunos : O que é espaço?
Após apresentarem suas hipóteses para a definição, conduza a discussão de forma a abordar que o espaço está relacionado com tudo o que nos envolve e é o local onde podemos nos mover para a frente, para o lado e para cima, ou seja, esse conceito relaciona-se a um ambiente tridimensional. Comente que nosso deslocamento no espaço pode ser expresso em linguagem matemática. Basta que nosso ponto de partida seja identificado como origem e depois indiquemos o quanto iremos nos deslocar para frente e para cima. Por exemplo: se um indivíduo está no centro da cidade em uma posição O=(0,0,0) e quer andar para a frente 3 quadras, depois andar para o lado 5 quadras e depois subir até o 10º andar de um prédio, a posição final do mesmo após o percurso será o ponto P=(3,5,10) *
*Este exemplo está disponível em http://pessoal.sercomtel.com.br/matematica/geometria/espaco/espaco.htm
Explique-lhes que, nesse caso, as direções também são indicadas como eixos, semelhantes ao que estavam usando para o deslocamento da aranha, só que agora, acrescenta-se mais uma dimensão, já que antes estavam trabalhando apenas com o conceito de andar para os lados. Comente que a Geometria espacial funciona como uma ampliação da Geometria plana. Os conceitos envolvidos são: pontos, retas, segmentos de retas, planos, curvas, ângulos e superfícies. Os principais tipos de cálculos realizados são: comprimentos de curvas, áreas de superfícies e volumes de regiões sólidas. (fonte: http://pessoal.sercomtel.com.br/matematica/geometria/element/element.htm).
Aponte que “atualmente, inúmeras profissões utilizam esses conceitos geométricos, entre elas pode-se citar: a engenharia, a arquitetura, a astronomia, as pesquisas nas ciências exatas, as atividades de uma costureira, de um mestre de obras, de um coreógrafo, de um artista plástico, de um atleta ou técnico. Sendo assim, a importância da Geometria é inquestionável, tanto sob o ponto de vista prático quanto do aspecto instrumental na organização do pensamento.” ( fonte: http://www.diaadiaeducacao.pr.gov.br/portals/pde/arquivos/2455-8.pdf)
Ofereça o seguinte texto para os alunos:
| Geometria Espacial Aplicada a Tecnologia Industrial: nas indústrias de moldados existem alguns dos exemplos mais comuns da aplicação dessa geometria. São usados moldes para fabricar todos os utensílios de plástico que são utilizados em nossas casas. Artigos tais, como recipientes, copos, lentes, caixas de computadores, armários de televisores, aparelhos, partes de automóveis e jogos são somente alguns dos produtos moldados de plástico. A geometria espacial é útil para determinar a quantidade de plástico necessária para preencher qualquer molde. Se calculada com precisão a quantidade de plástico necessária para fazer certa peça, pode-se encher o molde completamente, sem sobras e manter o custo de produção o mais baixo possível. Geometria Espacial Aplicada ao Comercio: frequentemente a indústria de embalagens exigem habilidades relativas à geometria espacial. Esta indústria é uma das indústrias modernas que está crescendo rapidamente. Praticamente tudo o que usamos nos chega dentro de algum tipo de embalagem. Jogos, aparelhos eletrônicos, produtos de beleza, produtos para o cuidado da saúde, produtos para uma fazenda, pinturas, adesivos, materiais de construção, alimentos e equipamentos esportivos, são apenas alguns exemplos de artigos embalados por este tipo de indústria. Todo artigo em três dimensões, deve ser embalado de forma eficaz e econômica. O material de embalagem, tal como o papelão, custa dinheiro. Perde-se dinheiro, quando se usa mais material de embalagem do que o necessário. Por isso, os desenhistas de embalagens sempre tratam de enviar a maior quantidade possível de produtos nos recipientes menores possíveis. A geometria espacial ajuda a resolver esse tipo de problema. Geometria Espacial Aplicada a Saúde: os tratamentos e procedimentos nas terapias respiratórias (pulmões), terapias cardíacas (coração) e terapias renais, usam volumes de fluídos. Frequentemente, o cálculo da velocidade de fluxo é crítico no tratamento apropriado dos pacientes. Os rins processam os fluídos do corpo permanentemente. Quando os rins deixam de trabalhar corretamente, o consumo de líquidos é maior que sua eliminação. Por isso o corpo incha e ocorrem graves problemas de saúde. As máquinas de diálise ajudam os rins doentes a filtrar os fluídos do corpo. Essa máquina funciona da seguinte maneira: em uma pessoa sadia, os rins processam e expelem aproximadamente 1500 cm3 de fluído de excreção para cada 2000 cm3 de fluído ingerido, em certo tempo. Porém, se uma pessoa tem problemas com os rins e ingere 2000 cm3, na pior das situações, os rins expelem somente 200 cm3, e, aproximadamente 1300 cm3 foram “armazenados”. Tal retenção causa forte inchaço do corpo e aumento de peso. Para eliminar o fluído em excesso, uma pessoa pode estar conectada a uma máquina de diálise dos rins. A máquina faz o sangue do corpo circular continuamente através da máquina e o devolve ao corpo. Este processo purifica o sangue (retira as impurezas) e expele o fluído de excreção, da mesma forma que os rins saudáveis fariam. A máquina retira bastante líquido para manter um peso estável. Para manter o equilíbrio entre o consumo de líquido e a eliminação, um paciente deve usar uma máquina de diálise cada 2 ou 3 dias. Cada seção com a máquina dura de 3 a 4 horas. Geometria Espacial Aplicada a Agricultura: a agricultura e negócios relacionados, usam a geometria espacial para determinar o volume (capacidade) de silos ou depósitos de armazenamento – para grãos, feno, palha, etc. Quando chega o tempo de colheita, devem conhecer a capacidade de armazenamento de silos e celeiros, além da capacidade de carga de caminhões e vagões dos trens. Quando chega o tempo de semear, o volume ou peso da semente disponível se relaciona com a área a ser semeada. Fonte: Verona, V. A e Lopes, M.R.M. Aplicação da Geometria Espacial em Ambientes Diversos.
Disponível em http://www.diaadiaeducacao.pr.gov.br/portals/pde/arquivos/2455-8.pdf |
Promova a leitura compartilhada do texto e estimule os comentários.
Em seguida, organize uma atividade prática para elaboração de conceitos. Em grupos de trabalho, os alunos deverão construir esqueletos de sólidos geométricos usando canudos. As orientações para esse trabalho encontram-se disponíveis no Portal do Professor em http://objetoseducacionais2.mec.gov.br/bitstream/handle/mec/10314/open/file/canudos.htm?sequence=18 .
Para essa proposta vocês deverão ter disponíveis: canudos plásticos de refrigerantes, em três cores (ou diâmetros) diferentes, um carretel de linha um pouco mais grossa do que a linha usada para empinar pipas, palitos “para churrasco”, anéis elásticos, e uma agulha grossa. No arquivo  Geometria com Canudos
Geometria com Canudos
disponível no Portal do Professor você encontrará a descrição detalhada para a produção dos esqueletos de sólidos geométricos. Assim, divida a turma em grupos e peça que cada um escolha uma das atividades para execução:
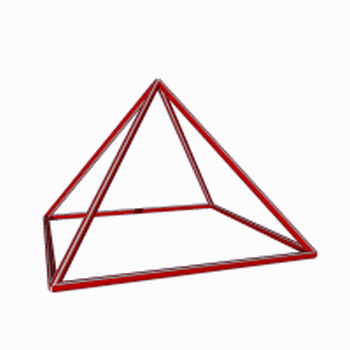
Pirâmide de base quadrada: 5 faces, 5 vértices e 8 arestas (8 canudos para construí-la)
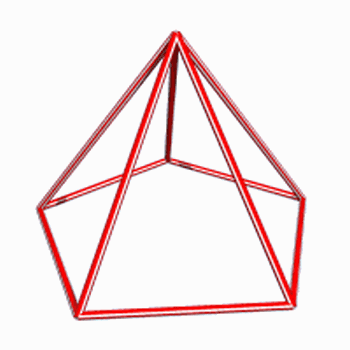
Pirâmide de base pentagonal: 6 faces, 6 vértices e 10 arestas (10 canudos para construí-la)
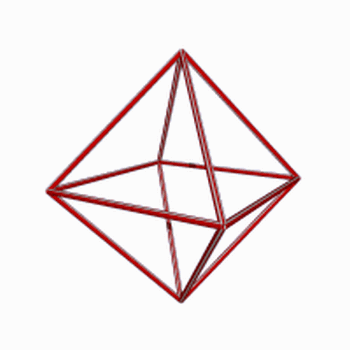
Octaedro: 8 faces, 6 vértices e 12 arestas ( 12 canudos para construí-lo)
Decaedro: 10 faces, 7 vértices e 15 arestas ( 15 canudos para construí-lo)
Icosaedro: 20 faces, 12 vértices e 30 arestas ( 30 canudos para construí-lo)
Depois peça que os grupos preparem-se para socializar os desafios da construção, usando o computador. Para isso, poderão produzir fotos e criar apresentações para subsidiar as explicações.
Orientações:
- Os alunos deverão usar os termos Vértice, Aresta e Face para as explicações. Assim, sugira que pesquisem mais sobre esses conceitos antes da apresentação.
- Deverão organizar uma apresentação usando imagens em 2D e 3D, com as fotos produzidas e esquemas para representação, inserindo -os em programas como o Power point.
Ofereça para consulta dos alunos a apostila Power Point , produzida pelo Centro de Computação da Unicamp, disponível em http://www.youblisher.com/files/publications/8/47190/pdf.pdf
| O Power Point oferece uma grande variedade de figuras predefinidas que podem ser desenhadas em seus slides.
Essas formas estão divididas em várias categorias: linhas, conectores, formas básicas, setas, etc., e podem ser livremente dimensionadas com o mouse e configuradas em suas propriedades de cor, sombra, contorno e 3D. Para inserir efeitos 3D, os alunos deverão selecionar com o mouse o objeto desejado e escolher o efeito a aplicar.
|
Em seguida, peça que em duplas, pesquisem mais sobre os termos e organizem uma explicação com os principais conceitos da geometria espacial:
- Como são definidas as posições relativas entre retas e planos
- Perpendicularismo
- Como podem ser medidas as distâncias e ângulos
Disponibilize o material  Geometria da Posição , disponível no Portal do Professor em http://portaldoprofessor.mec.gov.br/fichaTecnica.html?id=19661 para a consulta dos alunos. Esse material apresenta um hipertexto sobre Geometria Espacial , apresentando algumas das definições indicadas e outras mais. Oriente que consultem outras fontes para depois organizarem as sínteses sobre os principais conceitos.
Geometria da Posição , disponível no Portal do Professor em http://portaldoprofessor.mec.gov.br/fichaTecnica.html?id=19661 para a consulta dos alunos. Esse material apresenta um hipertexto sobre Geometria Espacial , apresentando algumas das definições indicadas e outras mais. Oriente que consultem outras fontes para depois organizarem as sínteses sobre os principais conceitos.
Ao final , promova uma discussão sobre as produções dos objetos tridimensionais e os conceitos pesquisados.
Para a conclusão das atividades, retome os principais conceitos abordados ao logo dessas aulas, utilizando as próprias produções em Power Point dos alunos para ilustrar onde esses conceitos podem ser visualizados.
Recursos Educacionais
| Nome | Tipo |
|---|---|
| Geometria com Canudos | Hipertexto |
| Teia Cartesiana | Animação/simulação |
| Geometria da Posição | Hipertexto |
Recursos Complementares
Conheça também o material: Varetas, canudos e arestas em sólidos Geométricos, produzidos por Ana Maria Kaleff e Dulce Monteiro Rei , disponível em http://portaldoprofessor.mec.gov.br/storage/materiais/0000011919.pdf .Nesse material há a descrição detalhada para a produção de outros esqueletos de sólidos geométricos, tais como o cubo e o tetraedro.
Avaliação
- Observe se os alunos compreenderam o conceito de plano cartesiano após o jogo Teia Cartesiana.
- Verifique se os alunos utilizam as noções geométricas espaciais como paralelismo, perpendicularismo, ângulo, direção, sentido, vértice, aresta, face, para descrever e representar as figuras que produziram .
- Promova uma reflexão entre os alunos sobre como trabalharam em duplas: foi produtivo? Como dividiram tarefas? Como poderiam organizar melhor o trabalho em uma próxima atividade? Essas questões são importantes para a tomada de consciência sobre o processo de aprendizagem e atuação em grupo, bem como para as suas intervenções nas organizações dos próximos agrupamentos.
Cinco estrelas 3 classificações
- Cinco estrelas 3/3 - 100%
- Quatro estrelas 0/3 - 0%
- Três estrelas 0/3 - 0%
- Duas estrelas 0/3 - 0%
- Uma estrela 0/3 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Claudia, E.E.B Profª Maria Garcia Pessi , Santa Catarina - disse:
claudiafrancs_@hotmail.com20/06/2014
Cinco estrelasmuito bom
-
Andre Hammacher, ESC MUN ENS FUN DOM PEDRO I , Rio Grande do Sul - disse:
andrehammacher@gmail.com01/08/2011
Cinco estrelasMuito bom! Pretendo usar alguns recursos desta aula.
-
danielle, danielle , São Paulo - disse:
d.vieira22@hotmail.com10/04/2011
Cinco estrelasotimo
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus