• Reconhecimento de raízes
• Gráficos de funções quadráticas
• O significado do coeficiente "a" na função f(x) = ax² + bx + c.

• Equações do 2° grau.

Para as atividades a seguir é necessário que a escola disponha de um laboratório de informática. E que obtenha o software livre Winplot que pode ser obtido no site: http://math.exeter.edu/rparris/winplot.html 

Este site está em inglês, caso tenha dificuldades acesse o site Baixaki:

http://www.baixaki.com.br/download/winplot.htm 

A instalação é fácil basta seguir as instruções.   

ATIVIDADE 1

No 1° momento fornecer uma lista de equações do 2° grau para os alunos resolverem. Exemplos de exercícios: x² - 5x + 6 = 0, x² + 2x + 1 = 0 e x² + 2x + 2 = 0.

É importante que o professor mostre várias formas de se resolver uma equação do 2° grau, no 1° exemplo o professor pode resolver usando soma (S = -b/a) e produto (P=c/a) das raízes, deve-se encontrar dois números em que a soma é 5 e o produto é 6, obtendo dessa forma os números 2 e 3 que são soluções da equação dada.

Depois o professor pode mostrar que x² - 5x + 6 pode ser fatorado como (x - 2)(x - 3) e portanto temos a equação escrita da forma (x - 2)(x - 3) = 0 e para o produto ser igual a zero x = 2 ou x = 3 o que nos fornce a solução da equação.

Uma outra forma de resolver é por completamento de quadrados escrevemos a equação na seguinte forma [x -(5/2)]² - (25/4) + 6 = 0, ou seja, [x -(5/2)]² - (25/4) + 6 = 0 que implica em [x -(5/2)]² = 1/4, mas os números que elevados ao quadrado dá 1/4 são 1/2 e -1/2 e portanto x - (5/2) = 1/2 ou x - (5/2) = -1/2 e assim obtemos x = 2 ou x=3 como solução.

E por último o professor deve resolver a equação com a conhecida "fórmula de Bhaskara". Depois utilizar as mesmas técnicas para os outros exemplos.

No 2° momento peça aos alunos para obterem funções cujas raízes são soluções da equação dada. Para isso deve-se recorrer  a forma fatorada y = a(x-x1)(x-x2), onde x1 e x2 são as raízes da função. Por exemplo, x² - 5x + 6 = 0 tem como solução x = 2 ou x = 3, como vimos acima.

Uma função que possui esses números como raízes é y = (x - 2)(x - 3), ou escrita de outra forma: y = x² -5x + 6. Podemos tomar a função y = 2(x-2)(x-3) ou, equivalentemente,

 y = 2x² -10x + 12 que possui 2 e 3 como raízes, isto é, as raízes são mantidas mas a abertura da parábola muda já que o valor de a em y = ax² + bx + c mudou.

ATIVIDADE 2 

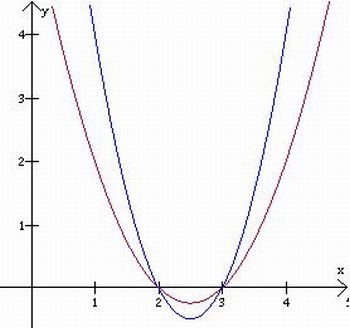
O professor deverá fazer o gráfico utilizando o Winplot e mostrar aos alunos que existem infinitas funções quadráticas que possuem as mesmas raízes de uma equação do 2° grau fornecida.Como no exemplo acima y = x² -5x + 6 e y = 2x² -10x + 12 possuem as mesmas raízes mas seus gráficos são distintos como mostra a figura a seguir

Imagem do autor

Em seguida passar uma lista de equações do 2° grau para que os alunos realizem o mesmo experimento, deve-se trabalhar nesse momento com os alunos o significado do coeficiente a na função f(x) = ax² + bx + c. Pode-se usar alguns exemplos anteriores e verificar que a abertura da parábola muda, ficando mais fechada a medida que o valor de a aumenta.

ATIVIDADE 3 

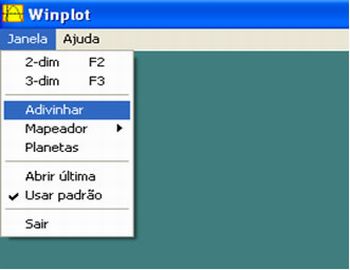
O aluno deverá usar o programa Winplot. Ao abrir o programa deverá clicar em Janela e depois clicar em Adivinhar.

Imagem do autor

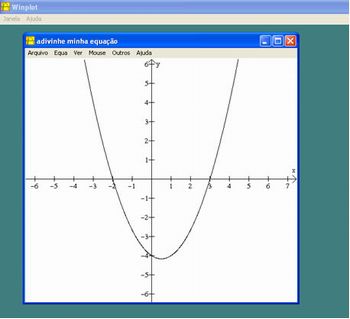
Após isso aparecerá na tela:

Imagem do autor

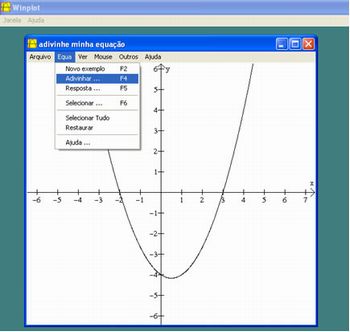
Através do gráfico o aluno terá que responder qual é a função cujo gráfico está representado pela figura acima. Para responder a pergunta o aluno deverá clicar em Equa e depois em Adivinhar. Ou se preferir apertar a tecla F4 do teclado, conforme mostra a figura a seguir.

Imagem do autor

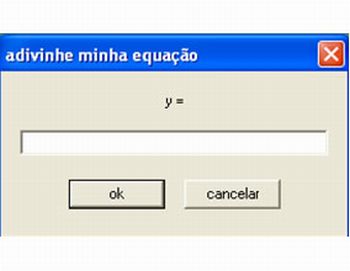
Após esses comandos aparecerá a janela:

Imagem do autor

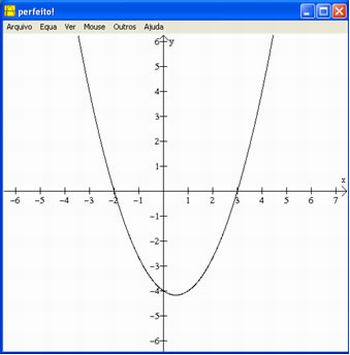
Digite a função e clique em OK. Caso o aluno acerte aparecerá escrito “perfeito” como mostra a figura:

Imagem do autor

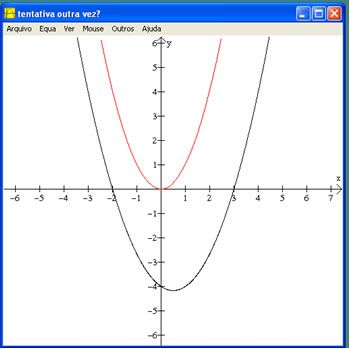
Caso contrário o programa mostra o gráfico da função que você digitou e escreve “tentativa outra vez?” como mostra a figura:

Imagem do autor

Para continuar com exemplos diferentes basta ir em “Equa” e clicar em “Novo Exemplo” ou apertar a tecla de atalho F2.

Aulas do Portal do Professor

Resolução de equações do 2º grau no CAp UFRJ  

(http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=9573)   

Equações do 2º grau no CAp UFRJ: Resolvendo via fatoração   

(http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=9517)  

Software livre Winplot que pode ser obtido no site:

http://math.exeter.edu/rparris/winplot.html  

ou

http://www.baixaki.com.br/download/winplot.htm    

Sugerimos que os alunos sejam avaliadas na execução da atividade com o Winplot.