08/02/2011
Rita Meirelles
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Artes | Música: Contextualização |
| Ensino Médio | Matemática | Números e operações |
| Ensino Médio | Artes | Arte Visual: Contextualização |
| Ensino Fundamental Final | Matemática | Grandezas e medidas |
O que o aluno poderá aprender com esta aula
Fractal e suas aplicações
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Sequências numéricas
Estratégias e recursos da aula

"Nuvens não são esferas, montanhas não são cones, continentes não são círculos, o som do latido não é contínuo e nem o raio viaja em linha reta."
(Benoît Mandelbrot, em seu livro "The Fractal Geometry of Nature" - 1983)
Fractais (do latim fractus, fração, quebrado) são figuras de uma geometria, elaborada pelo matemático polonês Benoit Mandelbrot, diferente da que estudamos convencionalmente nas escolas (a Geometria Euclidiana). Um fractal é um objeto geométrico que pode ser dividido em partes, cada uma das quais com a presença de características semelhantes ao objeto original. Os mais conhecidos são auto-similares, independem de escala e podem ser gerados por um padrão matemático repetido n vezes. A geometria fractal é usada para descrever muitas situações onde a Geometria Euclidiana "encontra" dificuldades por conta da complexidade a ser considerada. O contorno dos litorais, nuvens, relevo, montanhas, turbulências, árvores, crescimento de populações, vasos sangüíneos, brônquios e bronquíolos podem ser descritos utilizando as propriedades dos fractais.

Como primeira atividade sugiro uma pesquisa sobre o tema no laboratório de informática. Os alunos deverão buscar, nos sites de pesquisa, informações sobre o tema. Sugiro os sites:
(http://www.insite.com.br/fractarte/artigos/superinteressante.php)
(http://pt.wikibooks.org/wiki/Matem%C3%A1tica_divertida/Fractais_e_o_infinitamente_pequeno)
(http://pt.wikipedia.org/wiki/Fractal)
Incentive-os a pesquisar pelos principais tipos de fractais:
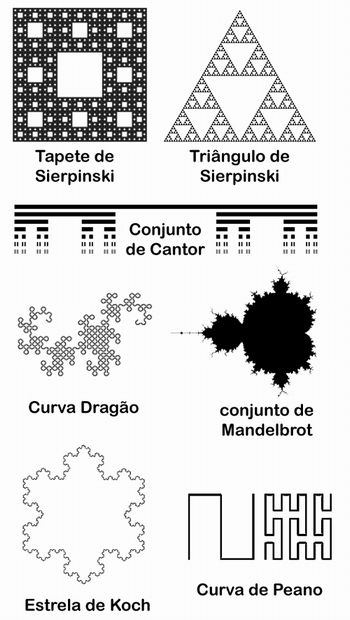
É importante que os alunos percebam a propriedade de auto-semelhança dos fractais, bem como a sua constatação na natureza. Para isso sugiro o vídeo:

Vídeo do autor disponível em (http://www.youtube.com/watch?v=wuZ7s7PL7Vc)
As imagens abaixo mostram este comportamento num tipo de couve-flor:

Disponível em (http://www.flickr.com/photos/28481088@N00/3181255999/)

Disponível em (http://www.flickr.com/photos/adamsfan/2668397504/)
O vídeo abaixo mostra um "zoom" num fractal baseado no conjunto de Mandelbrot. Repare a constante repetição de um padrão gráfico.
Disponível em (http://www.youtube.com/watch?feature=player_embedded&v=WAJE35wX1nQ#)
Sugiro também uma pesquisa sobre artes visuais com fractais. Indico as galerias:

Disponível em (http://www.insite.com.br/fractarte/galeria2/galeria.php)

Disponível em (http://galeria-arte-e-manhas.blogspot.com/2009/06/fractais-3d-lindas-imagens-feitas-com.html)

Disponível em (http://sobredotado.com/arte-digital-mainmenu-42/wallpapers-2d-mainmenu-46/146-a-arte-fractal-)

Disponível em (http://www.flickr.com/photos/011art/2368643947/)
E para finalizar, podemos também abordar o uso de fractais na música. Os alunos podem experimentar duas músicas em: (http://materialguilherme.webnode.com.br/news/musicas-fractais-/)
Para finalizar, faça um fórum onde cada aluno poderá expor seus achados.

Nesta segunda atividade proponho a criação de alguns fractais pelos alunos. Ainda no laboratório de informática, sugiro o uso do software:
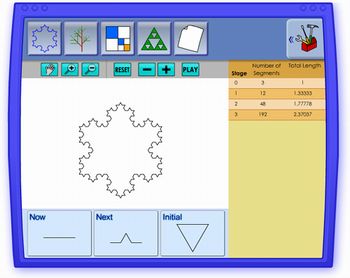
Disponível em (http://illuminations.nctm.org/ActivityDetail.aspx?ID=17)
O software é muito simples. Para visualizar os fractais basta selecionar um dos tipos disponíveis (botões grandes no topo do aplicativo) e clicar no botão play. Porém, o software oferece o recurso onde o próprio aluno poderá criar seus prórprios fractais. Veja como é simples:

Vamos fazer um exemplo:
Peça para os alunos clicarem no botão que tem o desenho de uma folha de papel em branco. O painel Now estará em destaque. Solicite que eles façam uma linha horizontal
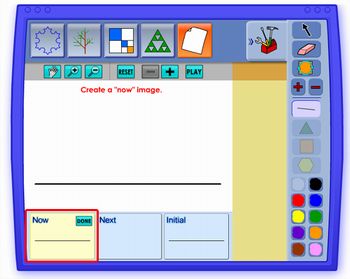
Peça agora para que eles clicarem no painel Next e reproduzirem o desenho abaixo
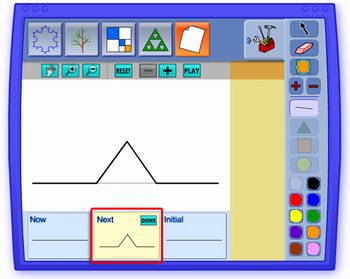
Agora é só clicar no botão "+" para ver cada etapa do fractal. Este fractal é conhecido como A Curva de Koch
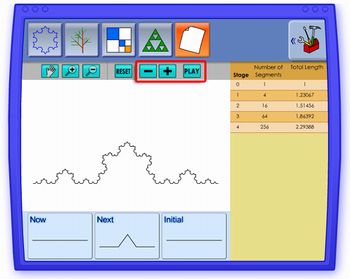
As possibilidades são infinitas. Deixe que os alunos experimentem livremente o software. Veja algumas idéias criativas abaixo:
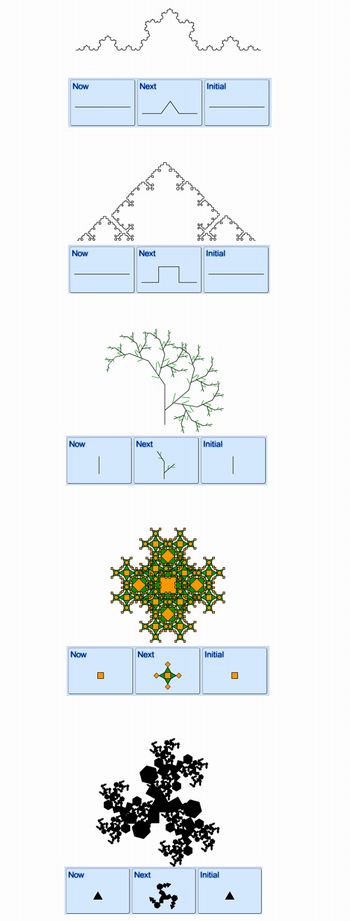
Na sala de aula, o professor pode propor outra atividade onde os alunos construirão um fractal numa folha de papel A4.
Veja como é simples:

Primeiramente, distribua uma folha de papel A4 para cada aluno. Acompanhe o processo:
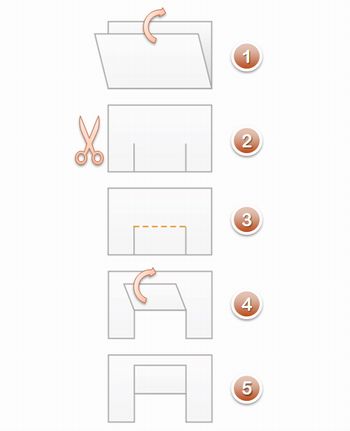
1) Dobre a folha ao meio;
2) Faça dois cortes como na figura;
3) A linha tracejada representa onde será feita uma dobra;
4) Dobre conforme a figura;
5) Esta é a primeira iteração do fractal.
Abra as dobras de maneira que fique como no desenho abaixo
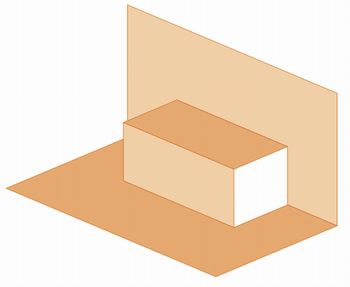
Vamos agora fazer outras iterações:
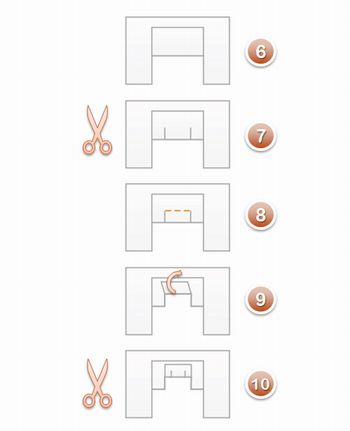
6) Dobre novamente como no último passo da sequência anterior;
7) Faça novamente dois corte como na figura;
8) Marca da dobra;
9) Dobre conforma a figura (está pronta a segunda iteração);

10) Voltando à dobra anterior pode se fazer o corte para a terceira iteração;
Veja o resultado na foto seguinte

Agora lance um desafio. Será que os alunos conseguem fazer mais uma iteração no papel?
Neste fractal sugiro uma análise. Peça para os deduzirem os dados da 4ª iteração. Veja a tabela.
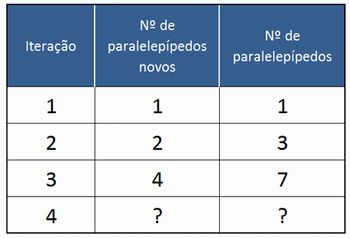
Repare que a quantidade de paralelepípedos novos a cada iteração pode ser representada por: 2n-1 , logo na iteração de número...
1 temos 21-1 = 1
2 temos 22-1 = 2
3 temos 23-1 = 4
4 temos 24-1 = 8
E assim por diante.
Claramente é uma PG de razão 2
Repare também que a quantidade de paralelepípedos totais de cada iteração é a quantidade de paralelepípedos da iteração anterior mais os novos paralelepípedos, logo...
a1 = 1
a2 = 1 + 2
a3 = 1 + 2 + 4
a4 = 1 + 2 + 4 + 8
E assim por diante.
Podemos afirmar que o termo geral desta sequência é igual a soma dos termos de uma PG onde a1 = 1 e q = 2. Veja:

Com essas informações, proponha o cálculo em outras iterações.

Para finalizar, o professor pode propor uma série de exercícios que abordam o tema. Veja o exemplo desta questão baseada numa questão do ENEM: (figuras adaptadas da prova do ENEM pelo autor)
Arte e técnica são igualmente necessárias para os profissionais que se dedicam à Topografia, que é a representação gráfica das formas e dos detalhes, naturais ou artificiais, de uma determinada região da superfície terrestre. Não é de hoje que os topógrafos se destacam na construção de edificações, estradas e barragens: há indícios arqueológicos de que os povos antigos já faziam uso das bases da Topografia. As pirâmides, por exemplo, são uma prova de que os antigos egípcios podiam executar medidas com boa exatidão.
Utilize as informações seguintes para responder aos testes de 1 a 3.
Entre os diversos tipos de brócolis, um dos mais sofisticados, pelo seu aspecto e sabor, é o romanesco, originário da Itália. Note que, na foto abaixo, a parte destacada é semelhante ao próprio brócolis romanesco e que mesmo as menores partes dele são semelhantes entre si. Essa repetição de padrões é muito comum na Natureza.

A Geometria Fractal (do latim fractus, fracionado, quebrado) é uma parte da Matemática que estuda, entre outras coisas, a repetição de padrões. Um fractal pode ser imaginado como uma figura constituída por figuras que se repetem indefinidamente… Observe a seguir o triângulo de Sierpinski, um fractal idealizado pelo matemático polonês Waclaw Sierpinski (1882-1969), em que a parte destacada é semelhante ao todo:
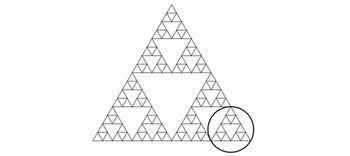
r
Considere as figuras seguintes:
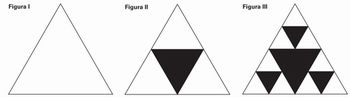
A figura II surgiu tomando-se os pontos médios dos lados do triângulo eqüilátero de superfície branca da figura I. A figura III surgiu tomando-se os pontos médios dos lados dos triângulos eqüiláteros de superfícies brancas da figura II. Note que, quando se tomam os pontos médios dos lados de um triângulo eqüilátero de superfície branca, surge bem no seu centro um triângulo eqüilátero de superfície preta. Desse modo, esse processo pode ser repetido várias vezes, indefinidamente, criando as figuras IV, V, …, que ainda não foram desenhadas.
1) Entre as alternativas seguintes, a que melhor representa a figura IV, que não foi desenhada aqui, é:

A resposta é a letra C. Discuta com seus alunos.
2) Sendo X a área do triângulo eqüilátero de superfície branca da figura I, a área da superfície preta na figura III é igual a:
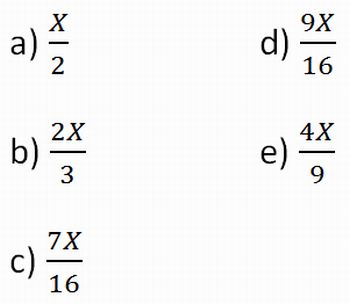
A resposta é a letra C. Discuta com os alunos soluções para esse problema.
3) Dentre as alternativas seguintes, a que melhor representa o número de triângulos eqüiláteros de superfícies brancas na figura V, que não foi desenhada no texto, é:
a) 27
b) 32
c) 36
d) 54
e) 81
A resposta é a letra E.
Colocarei agora outras questões baseadas em questões de vestibulares para serem discutidas entre os alunos.
Universidade de Brasília
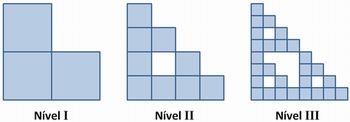
A sequência de figuras acima ilustra 3 passos da construção de um fractal utilizando-se como ponto de partida um triminó — nível I —, que consiste em uma peça formada por três quadradinhos de 1 cm de lado cada, justapostos em forma de L. No segundo passo, substitui-se cada quadradinho do fractal de nível I por um triminó, que tem os comprimentos dos lados de seus quadradinhos adequadamente ajustados à situação, de forma a se obter o fractal de nível II, conforme ilustrado acima. No terceiro passo, obtém-se, a partir do fractal de nível II, também substituindo-se cada um de seus quadradinhos por um triminó com os lados de seus quadradinhos ajustados, o fractal de nível III. O processo continua dessa forma, sucessiva e indefinidamente, obtendo-se os fractais de níveis n = I, II, III, ....
Com base nessas informações, calcule:
1) O perímetro externo do fractal de nível VI.
2) Uma expressão que represente a área do fractal de nível V.
3) O desenho do fractal no nível IV.
(UFRJ) A região fractal F, construída a partir de um quadrado de lado 1cm, é constituída por uma infinidade de quadrados e construída em uma infinidade de etapas. A cada nova etapa consideram-se os quadrados de menor lado (L ) acrescentados na etapa anterior e acrescentam-se, para cada um destes, três novos quadrados de lado L/3. As três primeiras etapas de construção de F são apresentadas a seguir.
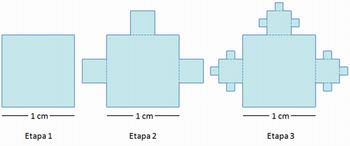
Represente, com uma expressão numérica, a área de F na 4ª etapa.
(UFF) Certas imagens captadas por satélites espaciais, quando digitalizadas, são representadas por formas geométricas de aspecto irregular ou fragmentado, conhecidas por fractais. Podem-se obter tais fractais pela alteração da forma original de uma curva por meio de um processo em que os resultados de uma etapa são utilizados como ponto de partida para a etapa seguinte. Considere o processo tal que, em todas as etapas, cada segmento de reta é transformado em uma poligonal cujo comprimento é quatro vezes a terça parte do segmento original, como ilustrado na figura a seguir:

Por esse processo, a partir de um quadrado com 1 metro de lado, obtém-se a seqüência de figuras:
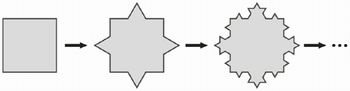
O perímetro, em metro, do quinto polígono dessa seqüência é:
a) 44 / 34 b) 44/35 c) 45/34 d) 35/ 45 e) 34/41

O tema Fractais desperta grande curiosidade nos alunos. Aproveite este interesse e mergulhe no tema.
Recursos Complementares
Para se aprofundar com seus alunos no tema, trabalhe a aula "Fractais no Ensino Médio" da Revista do Professor de Matemática, disponível, entre outras, em:
(http://www.rpm.org.br/cms/index.php?option=com_content&view=article&id=50&Itemid=58)
Avaliação
Todas as atividades propostas são ricas em oportunidades de avaliação. Acompanhe o desenvolvimento das tarefas e questione, sempre que achar necessário, os alunos.
Quatro estrelas 11 classificações
- Cinco estrelas 9/11 - 81.82%
- Quatro estrelas 1/11 - 9.09%
- Três estrelas 0/11 - 0%
- Duas estrelas 0/11 - 0%
- Uma estrela 1/11 - 9.09%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
daniela mendes vieira da silva, SEEDUC RJ , Rio de Janeiro - disse:
danielamvds@yahoo.com.br12/05/2014
Cinco estrelasShow, adorei!
-
Rarissa, Apeles Poa , Rio Grande do Sul - disse:
love_rari@hotmail.com12/07/2013
Uma estrelaMuito emocionante. Chorei. Mas tenho um professor ao qual sua metodologia não me transparece o que preciso. Estou no primeiro ano do segundo grau e não sei nada de física. Obrigada pela atenção.
-
Hanna Puertas, alternativa , Rio de Janeiro - disse:
hanna.puertas@hotmail.com23/05/2013
Cinco estrelasajudou bastante no tralho de matematica é um tema divertido
-
Elizety Mieko T. Kumagai, SEED/NRE Umuarama , Paraná - disse:
elizety@seed.pr.gov.br26/03/2013
Cinco estrelasParabéns professor! Achei muito interessante e prática a explicação.
-
DirceM, CE João Mazzarotto , Paraná - disse:
mathcjm@gmail.com11/11/2012
Quatro estrelasProfessor! Parabéns pela aula. Achei muito interessante e muito bem explicada.
-
Chronno, UFRN , Rio Grande do Norte - disse:
bido@click21.com.br08/11/2012
Cinco estrelasMuito interessante e elucidativa, e sua riqueza de detalhes proporciona uma boa assimilação do assunto. Parabéns
-
PAULO MURILLO DOS SANTOS, Colégio Integrado Jaó. , Goiás - disse:
paulo_matematico@hotmail.com17/10/2012
Cinco estrelasFantásitco
-
Luciane Silva, ________________________________________________ , São Paulo - disse:
crystallumspace@hotmail.com31/08/2012
Cinco estrelasAdorei! Muito obrigada!
-
Valéria Marques, UFRRJ , Rio de Janeiro - disse:
marquesvaleria@globo.com18/08/2012
Cinco estrelasExcelente, a iniciativa, a organização, a proposta, parabéns!
-
thaysa, .. sem instituição , Goiás - disse:
lyma_thaysa@hotmail.com25/06/2011
Cinco estrelasÓtimo site. Elucidativo. Encontrei após ter ficado muito curiosa em função de assitir o video The life secret of chaos produzido pela BBC. Nele é discutido o fractal. Estava procurando o fractal de Mendelbrot. Excelente!
-
Jussara, NTE Caxias , Rio de Janeiro - disse:
JCSOUZA28@GMAIL.COM21/03/2011
Cinco estrelasACHEI MUITO DINÂMICA, MOTIVADORA E RICA
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus


