06/06/2011

|

|

|

|

|

|

|

|

|

|
Alana Souza de Oliveira
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Fundamental Final | Matemática | Equações |
| Ensino Fundamental Final | Matemática | Álgebra |
O que o aluno poderá aprender com esta aula
- Compreender como se estabelece o ranking de uma competição;
- Reconhecer uma equação do 1º grau;
- Resolver equações do 1º grau.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
- Operações básicas com números inteiros.
Estratégias e recursos da aula
AMBIENTE 1/ATIVIDADE 1: Sala de aula
PREPARAÇÃO DO AMBIENTE:
Para a realização das atividades 1 e 2 serão utilizados: cartolinas, canetinhas coloridas, fita adesiva, quadro branco e pincel.
DESCRIÇÃO DA ATIVIDADE:

Fonte: http://www.skatecultura.com/2011/05/skate-nas-olimpiadas-do-rio.html
“Origem - Em cerca de 2500 a.C., os gregos realizavam festivais esportivos em honra a Zeus no santuário de Olímpia – o que originou o termo olimpíada. O evento era tão importante que interrompia até as guerras. Os nomes dos vencedores das competições começam a ser registrados a partir de 776 a.C. Participavam apenas os cidadãos livres, disputando provas de atletismo, luta, boxe, corrida de cavalo e pentatlo (que incluía luta, corrida, salto em distância, arremesso de dardo e de disco). Os vencedores recebiam uma coroa de louros. Mais tarde, os atletas se profissionalizam e passam a receber prêmios em dinheiro. As Olimpíadas perdem prestígio com o domínio romano na Grécia, no século II a.C. Em 392, o imperador Teodósio I converte-se ao cristianismo e proíbe todas as festas pagãs, inclusive as Olimpíadas. Era Moderna - A versão moderna dos festivais esportivos gregos é realizada, pela primeira vez, em 1896, em Atenas, por iniciativa do francês Pierre de Fredy (1863-1937), o barão de Coubertin. Participam 285 atletas de 13 países, disputando provas de atletismo, ciclismo, esgrima, ginástica, halterofilismo, luta livre, natação e tênis. Os vencedores são premiados com medalha de ouro e ramo de oliveira. Adota-se o termo "olimpíadas", no plural, pois na competição cada modalidade é encarada como uma olimpíada em separado.”
Fonte:http://www.portalbrasil.net/esportes_olimpiadas
Inicialmente, sugere-se que o professor leia e discuta com os alunos o texto acima, destacando os tipos de premiações ofertadas ao longo do tempo nessa competição.
Em seguida, o professor deverá propor o seguinte questionamento:
Qual país obterá melhor classificação nas Olimpíadas: aquele que conquista três medalhas de ouro e uma de prata ou aquele que consegue oito medalhas de bronze?

Fonte: http://websmed.portoalegre.rs.gov.br/escolas/robotica/obr2011/premiacoes.htm
Após uma discussão sobre as opiniões dos alunos acerca do questionamento acima, o docente deverá propor à turma, organizada em quatro grupos, a seguinte atividade:
Cada grupo deverá escolher um dos países, construir numa cartolina a tabela correspondente ao país escolhido e preencher os campos das duas últimas colunas da tabela “QUADRO DE MEDALHAS CONQUISTADAS”.
Para preencher a coluna “PONTUAÇÃO DE CADA MEDALHA”, basta atribuir uma quantidade de pontos a cada tipo de medalha e para preencher a coluna “TOTAL”, é preciso calcular a pontuação final do país correspondente.
| QUADRO DE MEDALHAS CONQUISTADAS |
||||||||
| PAÍS |
OURO |
PRATA |
BRONZE |
TOTAL DE MEDALHAS |
PONTUAÇÃO DE CADA MEDALHA |
TOTAL |
||
| CHINA |
10 |
5 |
2 |
17 |
O |
P |
B |
______ |
| ____ |
____ |
____ |
||||||
| QUADRO DE MEDALHAS CONQUISTADAS |
||||||||
| PAÍS |
OURO |
PRATA |
BRONZE |
TOTAL DE MEDALHAS |
PONTUAÇÃO DE CADA MEDALHA |
TOTAL |
||
| E.U.A |
6 |
6 |
6 |
18 |
O |
P |
B |
________ |
| ____ |
____ |
___ |
||||||
| QUADRO DE MEDALHAS CONQUISTADAS |
||||||||
| PAÍS |
OURO |
PRATA |
BRONZE |
TOTAL DE MEDALHAS |
PONTUAÇÃO DE CADA MEDALHA |
TOTAL |
||
| AUSTRÁLIA |
6 |
3 |
5 |
14 |
O |
P |
B |
_______ |
| ____ |
____ |
___ |
||||||
| QUADRO DE MEDALHAS CONQUISTADAS |
||||||||
| PAÍS |
OURO |
PRATA |
BRONZE |
TOTAL DE MEDALHAS |
PONTUAÇÃO DE CADA MEDALHA |
TOTAL |
||
| BRASIL |
0 |
0 |
2 |
2 |
O |
P |
B |
________ |
| ____ |
____ |
____ |
||||||
MOMENTO DO ALUNO:
Este é o momento em que os alunos desenvolverão a atividade proposta pelo professor.
DISCUSSÃO:
Cada grupo deverá fixar a sua tabela no quadro branco e expor suas soluções, com os devidos cálculos. Em seguida, os alunos deverão estabelecer um ranking com estes países. Caso os grupos tenham atribuídos valores diferentes para cada tipo de medalha (ouro, prata e bronze) o professor deverá discutir com eles sobre a impossibilidade de estabelecer um ranking com pesos diferentes para cada medalha, e então estabelecer uma pontuação única para cada medalha e organizar um novo ranking dos países em questão.
SISTEMATIZAÇÃO:
Com o objetivo de formalizar a ideia de “premiação” utilizada em competições de um modo geral, o professor deverá propor os seguintes questionamentos: Considerando os aspectos abordados no estabelecimento do ranking no momento anterior, é possível um país com nenhuma medalha de ouro ficar melhor colocado do que um país com uma medalha de ouro? Espera-se que os alunos considerem o aumento nas pontuações de medalhas de prata e ouro para compensar a pontuação de medalhas de ouro, convém lembrar que o professor deverá esclarecer que no ranking oficial das Olimpíadas isso não seria possível, pois o valor de uma medalha de ouro não é superado por qualquer quantidade de medalhas de prata ou de bronze.
AMBIENTE 1 / ATIVIDADE 2: Sala de aula
DESCRIÇÃO DA ATIVIDADE:
Ainda com a turma organizada em grupos, o professor deverá propor a seguinte atividade:
Calcule a pontuação atribuída à medalha de bronze que torna válido o total de pontos apresentado na tabela QUAL É A PONTUAÇÃO DA MEDALHA DE BRONZE? Que deverá ser registrada no quadro branco.
Observação: Cada grupo deverá escolher um dos países, ficando a critério dos mesmos a permanência com o país escolhido anteriormente.
| QUAL É A PONTUAÇÃO DA MEDALHA DE BRONZE? |
||||
| PAÍS |
OURO (Pontuação = 2) |
PRATA (Pontuação = 1) |
BRONZE (Pontuação = ?) |
TOTAL DE PONTOS |
| BRASIL |
10 |
5 |
4 |
45 |
| E.U.A |
5 |
2 |
4 |
32 |
| CHINA |
4 |
3 |
2 |
21 |
| AUSTRÁLIA |
4 |
2 |
1 |
15 |
MOMENTO DO ALUNO:
Os alunos buscarão realizar a atividade proposta.
DISCUSSÃO:
Os grupos apresentarão as suas soluções. Professor e alunos deverão discutir as estratégias de cada grupo para determinar seus resultados, como também as dificuldades encontradas durante a realização dessa atividade.
SISTEMATIZAÇÃO:
Nesse momento, o professor deverá denominar a expressão referente aos cálculos efetuados (Exemplo, no caso do Brasil, 10.2 + 5.1 + 4.x = 45) como equação do 1º grau e o valor desconhecido como variável dessa equação, e ainda que o seu grau é determinado pelo expoente dessa variável.
Com o intuito de apresentar a unicidade do valor da variável numa equação do 1º grau, o professor deverá discutir com os alunos a resposta para o seguinte questionamento: É possível encontrar mais de um valor para o peso da medalha de bronze que torne válida a totalização de pontos apresentada na tabela QUAL É A PONTUAÇÃO DA MEDALHA DE BRONZE?
AMBIENTE 2 / ATIVIDADE 3: Laboratório de Informática
PREPARAÇÃO DO AMBIENTE:
Para a realização desta atividade serão necessários: quadro branco, pincel e o material proposto pelo experimento Pescaria de equação do 1º grau (disponível em: http://objetoseducacionais2.mec.gov.br/handle/mec/3544) .
O Experimento prático Pescaria de Equações do 1º Grau trata-se deum baralho de equações (20 cartas) em cor amarelo e baralho de raízes em cor azul para formar os “lagos” de cartas (ver arquivo anexo).
DESCRIÇÃO DA ATIVIDADE:
Com os alunos divididos em trios e após a confecção das cartas amarelas e azuis formando o baralho de equações e o baralho de raízes (oprofessor deverá ter uma idéia aproximada de quantos trios serão formadospara saber quantas cartas deverão ser confeccionadas), o professor deverá distribuir os dois baralhos para cada grupo e convidá-los a explorar o experimento Pescaria de Equações do 1º Grau.
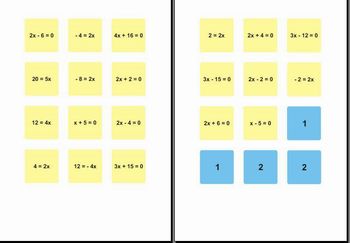
Fonte:Imagem do Autor
Observação: Antes do início da atividade o professor deverá ler com os alunos o arquivo o objetivo e as regras do experimento (arquivo em anexo).
MOMENTO DO ALUNO:
Nesse momento os alunos deverão explorar o experimento proposto.
DISCUSSÃO:
O professor deverá solicitar aos trios que exponham o modo como resolveram as equações do baralho e discutir com eles as dificuldades encontradas durante a realização da atividade.
SISTEMATIZAÇÃO:
Com o objetivo de formalizar a identificação e resolução de equações do 1º grau, o professor deverá sortear um aluno para ir ao quadro branco escrever uma equação ou uma raiz desse tipo de equação, em seguida outro aluno será sorteado para determinar o valor da raiz, caso o aluno anterior tenha escrito uma equação, ou então escrever uma equação caso o aluno anterior tenha escrito uma raiz, e assim ocorrerá até que todos os alunos tenham sido sorteados.
Recursos Educacionais
| Nome | Tipo |
|---|---|
| Pescaria de equação do 1º grau | Animação/simulação |
Recursos Complementares
http://objetoseducacionais2.mec.gov.br/handle/mec/3813 -Neste link encontra-se o objeto educacional “Equações do primeiro grau” que aborda o conceito de equações por meio de algumas situações em uma balança de dois pratos.
Avaliação
Na atividade 1 recomenda-se que o professor averigúe se os alunos conseguiram compreender como podem ser realizadas as premiações assim como o estabelecimento do ranking em uma competição. Na atividade 2, sugere-se verificar se os alunos conseguiram reconhecer equações do 1º grau e a sua aplicação em uma situação-problema. Já no caso da terceira atividade, o professor poderá identificar se os alunos conseguiram resolver as equações do primeiro grau.
Quatro estrelas 1 classificações
- Cinco estrelas 0/1 - 0%
- Quatro estrelas 1/1 - 100%
- Três estrelas 0/1 - 0%
- Duas estrelas 0/1 - 0%
- Uma estrela 0/1 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Edna Bandeira, Escola Telina Barbosa da Costa , Ceará - disse:
ednaufc@yahoo.com.br06/07/2011
Quatro estrelasGostei muito da forma dinâmica de se trabalhar equações do 1º grau. A atividade 1 mostra para o aluno que situações do cotidiano podem ser resolvidas através da Matemática e a atividade 2 mostra uma forma diferente e dinâmica de resolver equações do 1º grau.
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus

