Construir e explorar o circuncentro de um triângulo;

Verificar a relação entre o segmento que une os pontos médios de dois lados de um triângulo e o seu terceiro lado;

Construir e explorar o ortocentro de um triângulo.

3 horas-aulas

Noções sobre geometria plana: reta, segmento de reta, ponto, ângulos, circunferência, ponto médio, paralelismo, mediatriz, altura e classificação de triângulos quanto aos ângulos.

PREPARAÇÃO DO AMBIENTE:

Para a realização das atividades 1 e 2 serão utilizados: computador, data show (alternativa: quadro branco e pincel) e o software geogebra, que se encontra disponível no Banco Internacional de objetos Educacionais:http://objetoseducacionais2.mec.gov.br/handle/mec/3538   .

Geogebra.Br 

 

 

 

Botões e opções do GeoGebra que serão utilizados nesta aula

 

• 6º botão/1ª opção: Círculo definido pelo centro e um de seus pontos

                   Ao clicar na janela de gráficos, o centro do círculo estará sendo marcado/ Arrastar o mouse pela tela, e escolher um segundo ponto. Para marcá-lo é só clicar novamente

                   na tela.

• 4º botão/1ª opção: Reta perpendicular

                  Para construir uma reta perpendicular a outra, deve-se clicar sobre a reta na qual deseja traçar a reta perpendicular e em seguida clicar no ponto onde deverá passar a reta

                   que deseja construir.

• 1º botão/1ª opção: Mover um objeto geométrico

                  Ao clicar sobre um objeto geométrico, este será movido para onde desejar. 

•  2º botão/3ª opção: Ponto Médio

                  Clicar no segmento que deseja encontrar o ponto médio.

• 5º botão/1ª opção: Polígono

                  Ao clicar na janela de gráficos, o primeiro ponto para construção do polígono estará sendo marcado / Arrastar o mouse pela tela, e escolher os outros pontos. Para marcá-los é

                 só clicar novamente na tela.

• 8º botão/3ª opção: Medir distância ou comprimento

                 Clicar nos pontos extremos da distância que se deseja medir.

• 8º botão/1ª opção: Medir Ângulo

                 Clicar nos segmentos que determinam o ângulo que se deseja medir.

• 4º botão/3ª opção: Mediatriz

                 Ao clicar na reta (ou entre pontos) que deseja calcular a mediatriz aparecerá um segmento que passa pelo ponto médio;

• 2º botão/2ª opção: Interseção de dois objetos

                Clicar na região (quando ela for encontrada os dois objetos ficarão em destaque na tela) que por simples visualização consideramos como sendo a interseção dos

                dois objetos em questão.

• 3º botão/2ª opção: Segmento definido por dois pontos

                Clicar na janela de gráficos. Esse clique determinará um dos extremos do segmento / Arrastar o mouse pela tela e escolher o outro extremo do segmento. Para marcá-lo é

                 só clicar novamente na tela.

Observação: Para renomear um ponto é só clicar com o botão direito do mouse neste, escolher a opção renomear e digitar a denominação desejada.

Recomenda-se que o professor reserve 20 minutos da aula para explicar aos alunos como manipular o software Geogebra.

 

AMBIENTE 1 : Laboratório de informática

ATIVIDADE 1

DESCRIÇÃO DA ATIVIDADE:

Com a turma dividida em duplas, o professor deverá propor aos alunos a seguinte atividade:

Utilizando o software Geogebra   faça o que se pede abaixo:

1) Construir um triângulo ABC;

2) Construir as mediatrizes desse triângulo;

3) Marcar o ponto de interseção (D) das mediatrizes;

4) O que se pode observar ao mover os vértices do triângulo ABC?

 

MOMENTO DO ALUNO:

Este é o momento em que os alunos buscarão realizar a atividade proposta.

DISCUSSÃO:

Os alunos deverão expor para o restante da turma as suas soluções e observações, como também as dificuldades encontradas durante a realização da atividade.

Após discutir com os alunos suas soluções, observações e dificuldades, o professor deverá propor o seguinte questionamento: Como foi observado ao executar o passo 4 (se durante a apresentação os alunos não comentarem que o circuncentro pode pertencer ao triângulo, é importante que o professor destaque esse aspecto) o ponto de interseção (D) pode pertencer ao triângulo, ser interno ou externo a este, assim qual seria a condição para que cada um desses casos ocorra?

O professor poderá utilizar a opção ângulo do GeoGebra ( ver o campo Botões e opções do GeoGebra que serão utilizados nesta aula)  para mostrar a relação do circuncentro com triângulos retângulos, acutângulos e obtusângulos.

 

                              

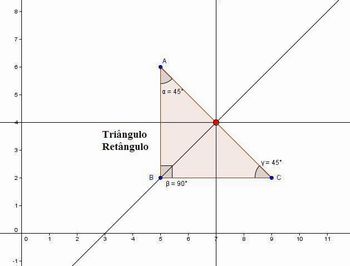
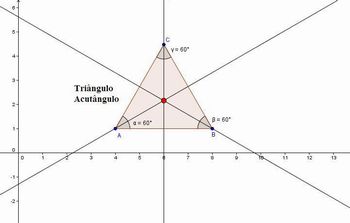
Fonte:Imagem do Autor                                                                        Fonte:Imagem do Autor

      

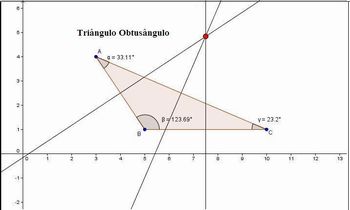
Fonte:Imagem do Autor

 

SISTEMATIZAÇÃO:

Com o objetivo de formalizar a construção e análise do circuncentro, recomenda-se que utilize o data show (alternativa: quadro branco e pincel) e construa com os alunos os três casos citados anteriormente para a localização do ponto de interseção das mediatrizes, denominando-o circuncentro. Em seguida, o professor deverá propor aos alunos o seguinte questionamento: observando estas construções, o que se pode verificar acerca da distância entre o circuncentro e os vértices?

Após as soluções dos alunos para esse questionamento, o professor deverá utilizar a opção distância do GeoGebra para medir as distâncias entre os vértices e os circuncentros dos triângulos, verificando que a distância entre o circuncentro de um triângulo e seus vértices são iguais, assim o professor deverá novamente questionar os alunos: qual é a figura geométrica formada a partir do circuncentro e dos vértices do triângulo?

Espera-se que eles respondam circunferência, e para mostrá-la o professor deverá utilizar a opção Círculo definido pelo centro e um de seus pontosdo GeoGebra (ver o campo Botões e opções do GeoGebra que serão utilizados nesta aula).

AMBIENTE 1: Laboratório de informática

ATIVIDADE 2

DESCRIÇÃO DA ATIVIDADE:

Ainda com a organização da turma em duplas, recomenda-se que o professor proponha aos alunos a seguinte atividade:

Utilizando o software Geogebra faça o que se pede abaixo:

1) Construir um triângulo ABC;

2) Marcar o ponto médio do lado AB e nomear com a letra M;

3) Marcar o ponto médio de AC e nomear com a letra N;

4) Construir o segmento MN;

5) Verificar as medidas dos segmentos MN e BC (É possível observar essas medidas na janela de álgebra (lado esquerdo da tela do GeoGebra);

MOMENTO DO ALUNO:

Este é o momento em que os alunos buscarão realizar a atividade proposta.

DISCUSSÃO:

Os alunos apresentarão para o restante da turma as suas soluções e observações, como também as dificuldades encontradas durante a realização da atividade.

SISTEMATIZAÇÃO:

Nesta etapa, recomenda-se que o professor formalize a relação entre os segmentos MN e BC. Inicialmente, ele deverá estimular os alunos a verificarem que os segmentos MN e BC são paralelos, e como foi verificado na atividade anterior o primeiro tem a metade da medida do segundo, e ainda denominar o segmento MN de base média do triângulo.

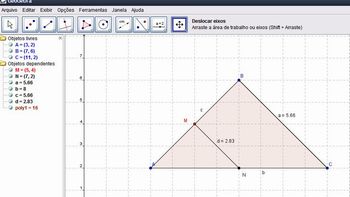
Fonte: Imagem do autor

 

Em seguida, o professor deverá solicitar aos alunos que movimentem os vértices A, B e C e observem as medidas dos segmentos MN e BC. Espera-se que os alunos verifiquem que a relação entre os segmentos MN e BC permanece, ou seja, a base média tem a metade da medida do lado BC, seja qual for o triângulo construído.

 

AMBIENTE 1 : Laboratório de informática

ATIVIDADE 3

PREPARAÇÃO DO AMBIENTE:

Para a realização da atividade serão utilizados o computador, o data show (alternativa: quadro branco e pincel) e a animação/simulação  “Alturas del triángulo y ortocentro” , que se encontra disponível no Banco Internacional de objetos Educacionais: http://objetoseducacionais2.mec.gov.br/handle/mec/15783   .

Alturas del triángulo y ortocentro 

 

 

 

DESCRIÇÃO DA ATIVIDADE:

Com a turma dividida em duplas, o professor deverá propor aos alunos a seguinte atividade:

Inicialmente, clique em VER DATOS TRIÂNGULO na parte superior do aplicativo, em seguida clique e movimente os vértices do triângulo.  

MOMENTO DO ALUNO:

Nesse momento os alunos buscarão realizar a atividade proposta.

DISCUSSÃO:

As soluções obtidas deverão ser apresentadas para o professor e o restante da turma. Durante ou após as apresentações, professor e alunos deverão discutir sobre as dificuldades encontradas durante a realização dessa atividade. Em seguida, caso os alunos não tenham comentado a relação entre a posição do ponto de interseção entre as retas e os ângulos que formam o triângulo, o professor deverá questioná-los sobre essa relação, analisando com eles os ângulos que são apresentados na tela na medida em que os vértices são movimentados, verificando que em triângulos acutângulos o ponto de interseção é interno e em triângulos obtusângulos o ponto de interseção é externo.

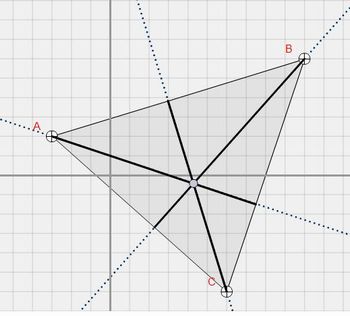
Triângulo Acutângulo

Fonte: Imagem do autor

 

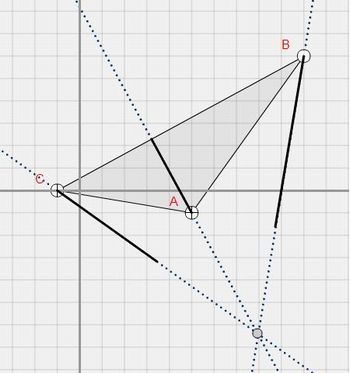
Triângulo Obtusângulo

Fonte: Imagem do autor

SISTEMATIZAÇÃO:

Nesta etapa, ocorrerá a sistematização da relação entre o posicionamento do ortocentro e os tipos triângulos. Será utilizado o data show (alternativa: quadro branco e pincel) para manipulação da animação/simulação “Alturas del triángulo yortocentro.

O professor deverá propor o seguinte questionamento aos alunos: qual é o nome atribuído a cada uma dessas retas que aparecem no aplicativo?

Espera-se que os alunos respondam que se trata de um triângulo, desse modo o professor denominará o ponto de interseção das alturas com o nome de ortocentro.

E em seguida, o docente deverá propor aos alunos o seguinte questionamento, é possível que o ortocentro pertença a um dos lados do triângulo? Em qual tipo de triângulo isso ocorre?

O docente deverá solicitar aos alunos que eles apresentem esse aspecto após a discussão sobre o questionamento proposto.

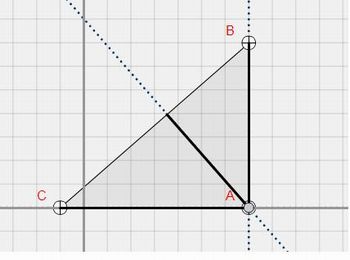
Triângulo Retângulo

Fonte: Imagem do autor

Nome	Tipo
Alturas del triángulo y ortocentro	Animação/simulação
Geogebra.Br	Software Educacional

http://clientes.netvisao.pt/arselio/Cindy0/triangulos.htm - O conteúdo deste site aborda os assuntos abordados nesta aula.

Sugere-se que o professor verifique na primeira atividade se os alunos conseguiram identificara relação entre a posição do circuncentro e os tipos de triângulos, e a existência da circunferência circunscrita ao triângulo.Na atividade 2, poderá ser averiguado se através  da construção geométrica  os alunos compreenderam a relação  entre o segmento que une os pontos médios de dois lados de um triângulo e o  terceiro lado desse triângulo. E na atividade 3, recomenda-se que o professor verifique se os alunos conseguiram relacionar os tipos de triângulos (acutângulo, obtusângulo e retângulo) e a posição do ortocentro.