20/08/2012
Paulo Antonio Silvani Caetano
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Números e operações |
| Ensino Médio | Matemática | Álgebra/Geometria |
| Ensino Médio | Matemática | Geometria |
O que o aluno poderá aprender com esta aula
O aluno aprenderá a reconhecer um progressão geométrica e a calcular um termo geral da progressão.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Cálculo de área de figuras planas, exponenciação.
Estratégias e recursos da aula
Antes da aula prepara triângulos equiláteros e quadrados de papel de tamanhos diferentes.
Inicie a aula separando a classe em grupos de 4 a 5 alunos e distribua uma figura de papel para grupo, de modo que haja um número de grupos com um quadrado igual ao número de grupos com triângulo.
Oriente cada grupo para que corte as figuras sem a ajuda de régua, apenas dobrando e marcando as figuras, da seguinte forma
.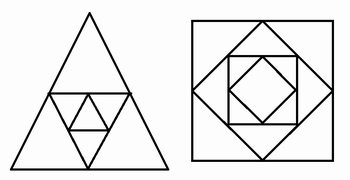
Em seguida faça o seguinte quadro e desenhe as seguintes figuras na lousa:
| Lado | A1 | A2 | A3 | A4 | A6 | A7 | An | |
| Grupo1 | ||||||||
| Grupo2 | ||||||||
| Grupo3 | ||||||||
| Grupo4 | ||||||||
| Grupo5 | ||||||||
| Grupo6 |
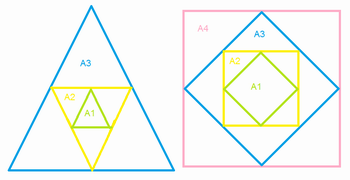
Peça que um membro de cada grupo copie o quadro, em seguida peça que cada grupo meça o lado de sua respectiva figura A1 e calcule sua área, e então preencha as colunas "lado" e "A1" da tabela junto aos alunos,
então peça que cada grupo tente calcular as áreas das figuras A2, A3 e A4 de sua respectiva figura cortada.
Peça que um grupo com quadrado tente calcular as áreas das figuras A2 e A3 de um grupo com triângulo, e peça que o grupo com o triângulo faça o mesmo com as figuras A2, A3 e A4 do grupo com quadrado. Faça isso com cada par de grupos.
Peça para que o grupo com quadrado diga o resultado encontrado e que o grupo com triângulo diga se está correto ou errado, e vice-e-versa, até que todas as linhas estejam preenchidas.
Fale com os alunos para que imaginem que eles possam aumentar as figuras para que elas pudessem ter mais cortes, peça para que cada par de grupos feitos anteriormente tente calcular a área de uma figura A6 do quadrado e de uma figura A7do triângulo. Preencha estas colunas da mesma forma como as anteriores, coletando os resultados e checando se está correto com os grupos.
Pergunte as alunos como eles chegaram em cada resultado, a anote as idéias na lousa, então debata com os alunos as similaridades e as diferenças de cada técnica, e introduza as noções de progressão geométrica junto ao debate.
Então com a ajuda dos alunos analise os resultados de cada progressão obtida pelo cálculo das áreas anteriores e com as idéias já expostas anteriormente, peça que tentem deduzir uma forma de calcular qualquer termo da progressão, e assim introduza ao cálculo do termo geral de uma progressão geométrica.
Recursos Complementares
Avaliação
A avaliação será feita através da participação do aluno na exposição de idéias e soluções do problemas. Além disso o professor pode pedir aos alunos que chequem a relação entre os lados das figuras afim de dizer se uma P.G., bem como pedir para que encontrem a formula do calculo do termo geral da possível P.G. dos lados.
Sem estrelas 0 classificações
- Cinco estrelas 0/0 - 0%
- Quatro estrelas 0/0 - 0%
- Três estrelas 0/0 - 0%
- Duas estrelas 0/0 - 0%
- Uma estrela 0/0 - 0%
Denuncie opiniões ou materiais indevidos!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus


