24/05/2013
Antomar Araújo Ferreira, Angela Cristina dos Santos
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Números e operações |
| Ensino Fundamental Final | Matemática | Grandezas e medidas |
O que o aluno poderá aprender com esta aula
- Adquirir a Competência de área 3 da Matriz do ENEM - Construir noções de grandezas e medidas para a compreensão da realidade e a solução de problemas do cotidiano;
- Desenvolver a habilidade H13 da Matriz do ENEM - Avaliar o resultado de uma medição na construção de um argumento consistente.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
- Reconhecer dimensões de um sólido: comprimento, largura e altura;
- Realizar medidas com régua;
- Calcular volume de um sólido: cubos ou paralelepípedos;
- Efetuar transformação de unidade de medida: m, dm, cm, mm;
- Efetuar transformação de unidade de volume: m³, dm³, cm³, mm³;
- Saber utilizar calculadora simples;
- Organizar dados em tabelas ou quadros.
Estratégias e recursos da aula
RECURSOS MATERIAIS
- Recipientes na forma de cubos e paralelepípedos;
- Régua milimetrada;
- Quadro para anotações dos valores a serem medidos e também para registro dos cálculos.
ESTRATÉGIAS
Professor, Inicie a aula com a leitura e discussão do texto disponível no site: <http://www.portalsaofrancisco.com.br/alfa/meio-ambiente-agua/agua-2.php>. Acesso em: 10 mai. 2013. Sugere-se que o professor possibilite aos alunos discutirem as questões apontadas no texto: Você acredita que, em poucas décadas, teremos dificuldades em encontrar água potável para nossa sobrevivência? A água é abundante no Brasil? A água é bem distribuída pelas regiões brasileiras? O que podemos fazer no nosso dia a dia para evitar o desperdício de água? O professor pode, ainda, sugerir novos questionamentos que julgar importante para a discussão do assunto. Espera-se que os alunos compreendam a importância de cuidarmos e preservamos nossas fontes de água e, assim, evitarmos o desperdício e a escassez de água. É importante que os alunos percebam que mesmo com pequenas mudanças de atitude podemos fazer a nossa parte e, desse modo, respeitarmos e preservamos o principal recurso responsável pela vida em nosso planeta.
Depois do momento de discussão, sugere-se que o professor aborde a importância das chuvas para a manutenção do nível de água dos reservatórios de água que abastecem as cidades e como estas dependem desses recursos, bem como as chuvas são as responsáveis pelo retorno da água à superfície terrestre e assim, à reposição da água destes reservatórios. É importante que o professor permita que os alunos expressem suas opiniões e considerações sobre o assunto.
Após essas atividades, sugere-se que o professor solicite que os alunos procurem notícias sobre o índice de chuvas da sua cidade e/ou região para a próxima aula ou momento (caso as aulas sejam geminadas, essa busca pode ser realizada também em sala de aula com o auxílio de um computador conectado à Internet). Espera-se que os alunos tragam notícias que usem o mm como unidades de medida.
Assim, recomenda-se que o professor questione os alunos sobre o que significam essas notícias, como um agricultor ou a população em geral entende essa informação. E ainda, quais são os produtos “líquidos” mais utilizados em casa e quais são as unidades de medida que esses produtos são comercializados (leite, óleo, creme de leite, entre outros). Espera-se com esses questionamentos que o professor consiga orientar os alunos a perceberem que as unidades mais usadas são as de capacidade (litro - L, mililitro - mL) e comumente, são empregadas como sinônimas de unidades de volume (m³, dm³, cm³, mm³), sendo que o volume é uma unidade de medida referente ao espaço ocupado por um determinado sólido geométrico, enquanto a capacidade refere-se à quantidade de armazenamento possível deste sólido. Professor, discuta com os alunos como verificar a capacidade da embalagem de um produto, como por exemplo, do leite longa vida, por meio do cálculo do volume da sua embalagem, uma vez que a informação que consta na embalagem refere-se à quantidade do produto comercializado. Aconselha-se ao professor a realização da demonstração de como calcular o volume de uma embalagem, como a do leite longa vida, como por exemplo:
Figura 1: Exemplo de como calcular o volume em embalagens

Fonte: imagem do autor
Professor, pergunte aos seus alunos qual a unidade de medida do volume que melhor representa o cálculo deste produto. E ainda, se o volume da embalagem é calculado em m³, cm³, dm³ ou mm³ e o produto é comercializado em unidades como o litro ou mililitro, como é realizada esta relação? A expectativa é que esses questionamentos despertem a curiosidade e motivem os alunos a realizarem as atividades propostas.
Após esses momentos, sugere-se que o professor divida a turma em duplas ou grupos de até 4 alunos e solicite que os alunos busquem como realizar o cálculo do volume de um sólido geométrico. Essa busca pode ser realizada com o uso do computador conectado à Internet. Professor, providencie para cada grupo ou dupla um sólido geométrico regular: cúbicos ou paralelepípedos com diferentes dimensões, como os representados na figura 2 a seguir.
Figura 2: Exemplos de recipientes

Fonte: imagem do autor
Posteriormente, solicite aos alunos que reconheçam as dimensões do sólido: comprimento, largura e altura e realizem as medidas dessas dimensões usando a régua milimetrada. Sugere-se, ainda, que o professor solicite aos discentes para anotarem os valores em um quadro ou tabela (quadro 1), como no exemplo a seguir. Propositalmente, deixe duas linhas do quadro ou tabela em branco.
Julga-se importante que o professor oriente seus alunos a adotarem uma unidade de medida inicialmente, seja cm ou mm e, posteriormente, efetuem as transformações entre diferentes unidades.
Quadro 1: Anotação dos valores medidos e calculados
| Dimensão |
Valor medido (metro) |
Valor medido (centímetro) |
Valor medido (decímetro) |
Valor medido (milímetro) |
| Comprimento |
|
|
|
|
| Largura |
|
|
|
|
| Altura |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Após o preenchimento do quadro ou tabela, o professor pode questionar os alunos para que eles percebam a regularidade na transformação entre as diferentes unidades de medida. E, assim, percebam que para efetuarem as transformações, basta apenas multiplicar ou dividir por 10, 100, 1000, ... Os alunos podem ser orientados a construírem o esquema a seguir (figura 3):
Figura 3: Transformação de unidades de comprimento
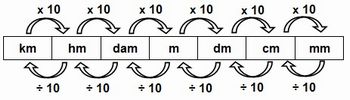
Fonte: imagem do autor
Julga-se importante que o professor questione os alunos sobre transformações entre os diferentes múltiplos e submúltiplos entre as unidades de medida, como por exemplo: metro em centímetro, metro em milímetro, quilômetro em metro, quilômetro em centímetro, entre outras.
Após as transformações entre as unidades de medida, sugere-se que o professor retome a tabela onde as medidas das dimensões dos sólidos foram anotadas e solicite que os alunos calculem, em cada caso, o volume de cada recipiente e anote os valores calculados em uma das linhas em branco. E, assim, anote os valores determinados.
Quadro 1: Anotação dos valores medidos e calculados
| Dimensão |
Valor medido (metro) |
Valor medido (centímetro) |
Valor medido (decímetro) |
Valor medido (milímetro) |
| Comprimento |
|
|
|
|
| Largura |
|
|
|
|
| Altura |
|
|
|
|
| Volume |
|
|
|
|
|
|
|
|
|
|
Após a realização dos cálculos e anotação dos valores no quadro ou tabela, pondera-se que o professor chame a atenção para que os alunos expressem o resultado com a unidade de volume adequada. Para isso, aconselha-se o resgate do conceito de potenciação e a sua representação – por exemplo, 5 x 5 = 5² e 5 x 5 x 5 = 5³ – e, em seguida, questionar com os alunos qual seria então a unidade de medida de volume. Espera-se que eles compreendam que quando as dimensões são expressas em metros (m), a unidade de volume é o metro cúbico (m³), pois equivale a m³ = m x m x m, se as dimensões são expressas em cm, o volume será cm³, e assim sucessivamente.
Após essas explicações, sugere-se que o professor retorne à tabela e questione os alunos para que estes percebam a regularidade na transformação entre as diferentes unidades de medida de volume. E, assim, percebam que para cada unidade de volume é 1000 vezes maior do que a unidade imediatamente inferior ou 1000 vezes menor do que a unidade imediatamente superior e para efetuarem as transformações entre as unidades basta multiplicar ou dividir por 1000, 1000000, 1000000000, ... Os alunos podem ser orientados a construírem o esquema a seguir (figura 4):
Figura 4: Transformação de unidades de volume
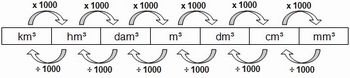
Fonte: figura do autor
A construção desse quadro é um momento oportuno para que o professor questione os alunos por que as transformações no primeiro quadro eram operações de por 10 e agora as multiplicações e divisões são por 1000. Espera-se com isso que os alunos percebam a relação com o número de dimensões em questão em cada caso.
ENRIQUEÇA SUA AULA
Como atividade final, proponha que os alunos procurem produtos que sejam comercializados em embalagens semelhantes aos sólidos estudados, conforme a figura a seguir e realizem as medidas e o cálculo do volume da embalagem escolhida.
Figura 5: Exemplos de embalagens

Fonte: figura do autor
Sugere-se que o professor solicite aos alunos a descrição das estratégias e dos procedimentos empregados para o cálculo do volume da embalagem escolhida na forma de um relatório. Essas embalagens também podem ser utilizadas na aula complementar a esta: "A relação entre volume e capacidade em sólidos geométricos: realizando a conversão ".
Recursos Complementares
Para medidas e cálculos mais precisos, sugere-se que o professor utilize paquímetros ao invés da régua.
Como os objetivos principais da aula não são os cálculos e sim a compreensão das estratégias de cálculo do volume, o professor pode aproveitar a aula e permitir o uso da calculadora. Como apontam os Parâmetros Curriculares Nacionais (PCN), recursos didáticos como as calculadoras desempenham um papel importante no processo de ensino e aprendizagem. Ainda conforme defende o PCN, “a calculadora pode ser utilizada como um recurso didático, tanto para que o aluno analise resultados que lhe são apresentados, como para controlar e corrigir sua própria produção” (BRASIL, 1999, p. 53).
O professor pode também, caso a aula seja para o Ensino Médio, variar os prismas usando modelos com diferentes bases, além de recipientes cilíndricos. Sugere-se que, para o Ensino Fundamental, o professor utilize formatos cúbicos e retangulares.
Caso seja interesse do professor aprofundar estudos sobre os índices pluviométricos, sugere-se o texto e o vídeo disponível em: <http://g1.globo.com/pernambuco/noticia/2011/10/projeto-educacao-mostra-como-funciona-na-pratica-o-pluviometro.html>. Acesso em: 03 mai. 2013.
Referências
BRASIL. Secretaria de Educação Fundamental. Parâmetros curriculares nacionais: matemática. Brasília: MEC/SEF, 1997.
Avaliação
Sugere-se que o professor realize a avaliação ao longo do desenvolvimento de todo o processo, observando o envolvimento dos alunos na realização das atividades propostas. Dessa forma, o professor pode avaliar pela motivação e empenho dos alunos na prática das ações solicitadas. Como critério de avaliação, sugere-se, ainda, que o professor solicite uma apresentação dos procedimentos e estratégias utilizadas por cada grupo. Além disso, o professor pode concretizar o processo avaliativo com uma autoavaliação realizada com a turma buscando sugestões dos alunos envolvidos e observando se os objetivos iniciais foram alcançados.
Cinco estrelas 2 classificações
- Cinco estrelas 2/2 - 100%
- Quatro estrelas 0/2 - 0%
- Três estrelas 0/2 - 0%
- Duas estrelas 0/2 - 0%
- Uma estrela 0/2 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Marília Barroso, E.E.Mons.José Amantino dos Santos , Minas Gerais - disse:
mariliaqalves@hotmail.com24/06/2014
Cinco estrelasótima aula.
-
Gabriel Urbano, Estudante de Matemática - UNIMES , São Paulo - disse:
gabriel_urbano1@yahoo.com.br17/06/2013
Cinco estrelasFico muito feliz com este canal aberto aqui no portal do professor, onde esta troca de conhecimentos nos torna mais e mais informados e aptos a um ensino de real qualidade. Adorei a aula e com certeza irei usar total ou parcialmente algumas idéias que tive a grande oportunidade de ler aqui. Muito obrigado por dividir conosco e parabéns!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus


