26/08/2009
Marco G. B. Burlamaqui
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Álgebra |
| Ensino Médio | Matemática | Geometria |
| Ensino Médio | Matemática | Números e operações |
O que o aluno poderá aprender com esta aula
Calcular o valor das funções trigonométricas de ângulos não pertencentes ao 1º quadrante, relacionando com algum elemento do 1º quadrante.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
• Círculo trigonométrico
• Definições de seno, cosseno e tangente no círculo trigonométrico
Estratégias e recursos da aula
Olá Professor, vamos apresentar alguns recursos para trabalhar o assunto “Redução ao primeiro quadrante” com seus alunos. Leve-os ao laboratório de informática e acomode-os em duplas. Antes de iniciar o assunto, faça os seguintes questionamentos:
• O que é um círculo trigonométrico?
• Como se define a função seno no círculo trigonométrico? E a cossecante?
• E a função cosseno? E a secante?
• E a função tangente? E a cotangente?
Caso ainda exista alguma dúvida, procure saná-las. Para isto você pode utilizar alguns sítios que tratam do assunto “Redução ao primeiro quadrante” e também uma revisão dos conhecimentos prévios, como exemplo:
• http://alfaconnection.net/pag_avsm/trg0201.htm#TRG020203
• http://pessoal.sercomtel.com.br/matematica/trigonom/trigo03.htm, neste leiam a definição seno, cosseno e tangente;
• http://www.klickeducacao.com.br/2006/materia/20/display/0,5912,POR-20-97-969-5211,00.html
Professor, para que os alunos possam fazer a análise dos diversos casos de redução para o primeiro quadrante, utilizaremos o GeoGebra, para consolidar os conhecimentos teóricos vistos nos links anteriores. Vamos realizar uma atividade no laboratório de informática utilizando um software de geometria dinâmica, http://www.geometriadinamica.com/, o GeoGebra. Ele é para se utilizar em ambiente de sala de aula. Ele reúne GEOmetria, álGEBRA e cálculo. Esta disponível em http://www.geogebra.org/ em versão para download gratuito ou para ser executado via web (WebStart).
No caso desta atividade, tenha instalado previamente o GeoGebra em todos os computadores do laboratório de informática. Como documentação do software, temos:
• O manual disponível em http ://www.geogebra.org/he lp/docupt_BR.pdf e outro http://www.geogebra.org/help/docupt_PT.pdf, este em português de Portugal, mas um pouco mais completo;
• Uma apostila sobre a utilização est a disponível em http://www.tinaeducacao.com.br/wp-content/uploads/2008/11/apostilageogebra_2007.pdf, nesta apostila temos várias atividades utilizando o software, e
• Um guia rápido de comandos, disponível em http://cattai.mat.br/site/files/geogebra/guia_rapido_geogebra.pdf.
Professor, vamos mostrar aos alunos maneiras de proceder o cálculo da funções trigonométricas de um ângulo que não pertence ao 1º quadrante, relacionando com um do 1º quadrante. Peça a eles que sigam os seguintes passos, para o 1º caso: Redução do 2º quadrante para o 1º quadrante ( π/2 < α < π).
Passo 1: Inicie o aplicativo GeoGebra, aparecerá a seguinte tela:
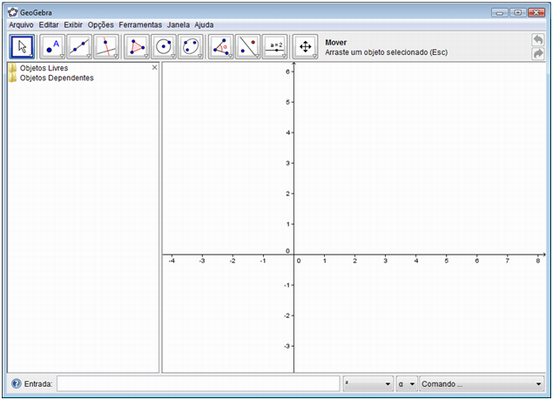
Professor, comente com seus alunos que na barra de botões,

temos diversas ferramentas que podem ser utilizadas. Em todos os botões aparece uma seta no canto inferior direito, que, ao ser clicada, permite visualizar as opções existentes.

Passo 2: Ampliar o campo de visão. No último botão da barra de botões, selecione a ferramenta “Ampliar” e clique na área de trabalho até que as medidas dos eixos x e y sejam as da figura abaixo. Em seguida, no mesmo botão, selecione a ferramenta “Deslocar eixos” e centralize o sistema de coordenadas cartesianas conforme a figura abaixo.
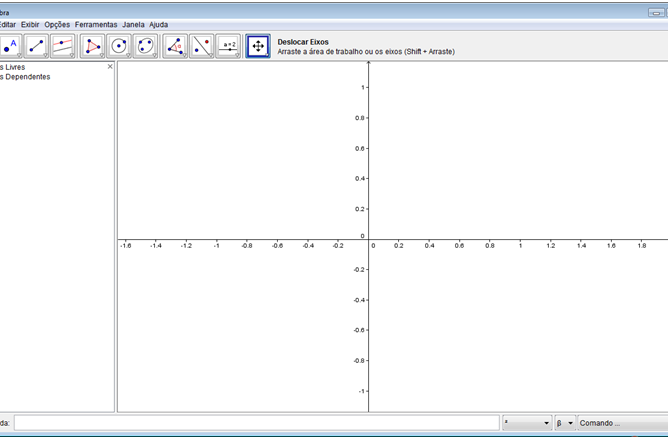
Passo 3: Criar um ponto A (0,0) na intersecção dos eixos x e y. No segundo botão da barra de botões, selecione a ferramenta “Novo ponto” e clique na intersecção dos eixos x e y. Existe outra forma de criar o ponto A. Na parte de baixo do aplicativo, existe uma caixa de texto destinada a entrada de dados e de fórmulas,
 .
.
Digite: A =(0,0).
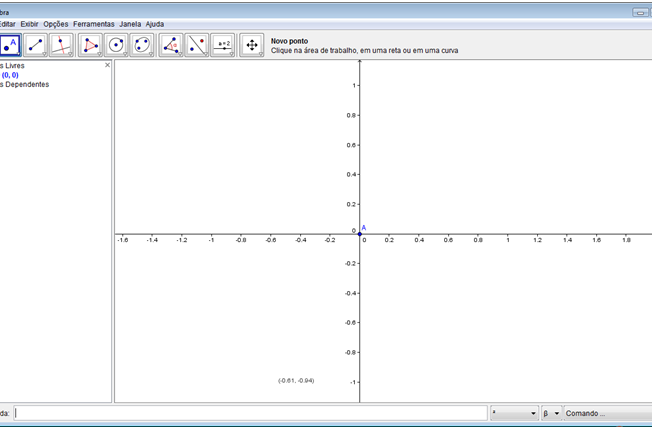
Passo 4: Criar um ponto B nas coordenadas (1,0).
Passo 5: Criar uma circunferência de centro em A passando por B. No sexto botão da barra de botões, selecione a ferramenta “Círculo dados centro e raio” e clique no ponto A e em seguida no ponto B. Para melhorar a visualização, no primeiro botão da barra de botões, selecione a ferramenta a opção “Mover”; cliquem no texto “c” e mova-o para fora da circunferência, como mostra a figura abaixo.
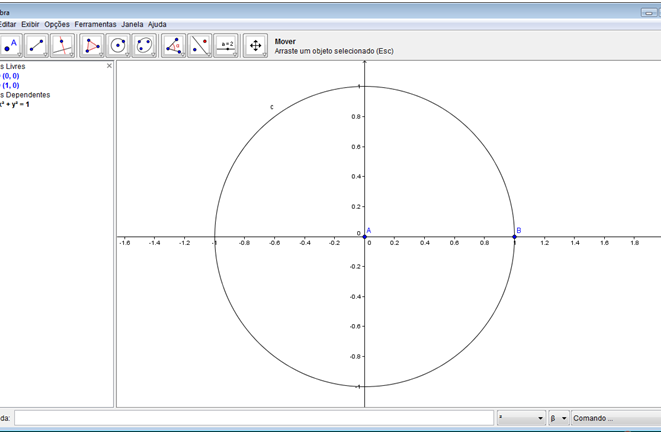
Passo 6: Criar um ponto C sobre a circunferência. No segundo botão da barra de botões, selecione a ferramenta “Novo ponto” e clique na circunferência na região do primeiro quadrante.
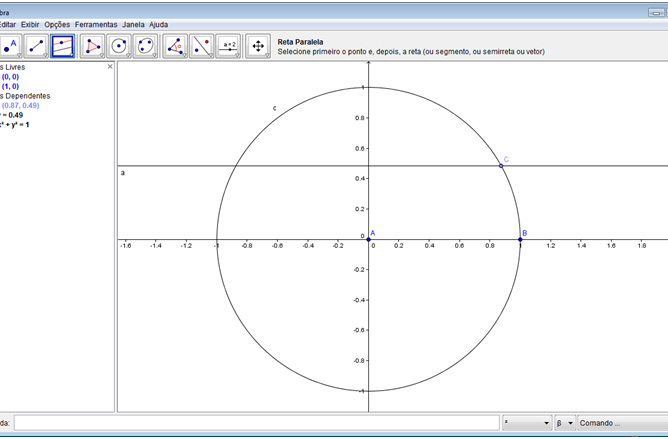
Passo 7: Criar uma reta “a” paralela ao eixo x que passa pelo ponto C. No quarto botão da barra de botões, selecione a ferramenta “Reta paralela” e clique no eixo x e em seguida no ponto C.

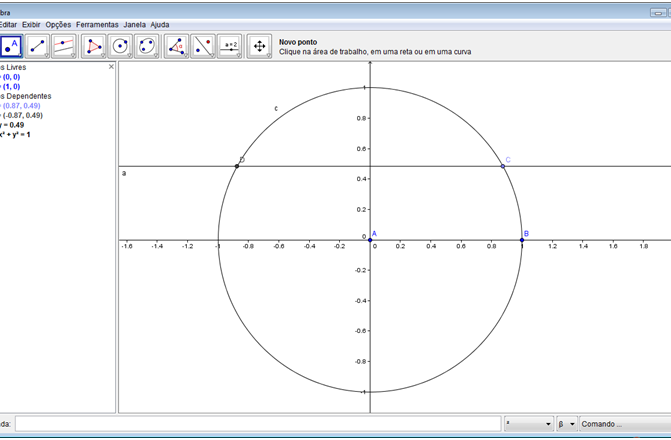
Passo 8: Criar um ponto D na intersecção da circunferência e a reta “a” no segundo quadrante do sistema de coordenadas cartesianas. No segundo botão da barra de botões, selecione a ferramenta “Novo ponto” e clique no ponto de intersecção da circunferência e a reta “a”, no segundo quadrante.
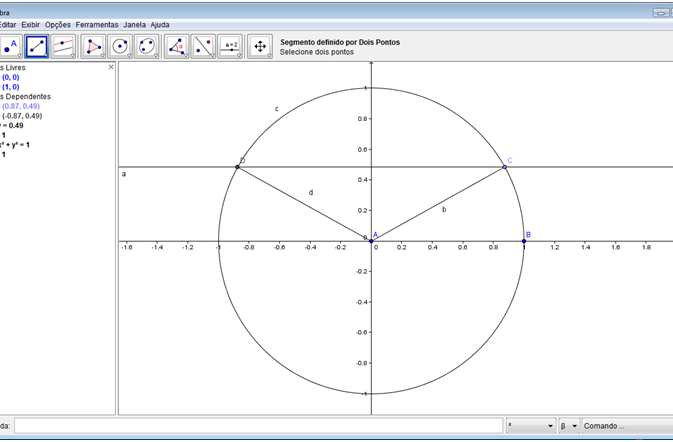
Passo 9: Criar segmento de reta ligando os pontos A e C; e outro ligando os pontos A e D. No terceiro botão da barra de botões, selecione a opção “Seguimento definido por dois pontos”, e em seguida, clique nos pontos A e C, em seguida nos clique nos pontos A e D. Observe que no lado esquerdo da tela aparece uma lista de objetos dependentes. Neste caso, temos agora os segmentos “b” e “d” com os valores de suas medidas em centímetros. Peça aos alunos que s elecione, no primeiro botão da barra de botões, a opção “Mover”; cliquem no ponto C e mova-o; e observe:
• O que acontece com as abscissas e ordenadas dos pontos C e D?
Passo 10: Determinar as medidas dos ângulos BAC e BAD. No oitavo botão da barra de botões, selecione a opção “Ângulo”, e em seguida, clique nos pontos B, A e C, nesta sequência. Em seguida, nos pontos B, A e D, nesta sequência. Crie também um ponto E em (-1,0). Peça aos alunos que selecione, no primeiro botão da barra de botões, a opção “Mover”; cliquem no ponto C e mova-o; e observe:
• O que acontece com a soma dos ângulos criados? Na parte de baixo do aplicativo, existe uma caixa de texto destinada a entrada de dados e de fórmulas,
 .
.
Na terceira caixa, selecione as letras do alfabeto grego e digite: γ=α+β. Observe na lista de objetos dependentes o valor de γ. Mova novamente o ponto C, o que acontece com o valor de γ?
• Como são classificados estes ângulos?
• As medidas dos ângulos BAC e EAD são iguais?
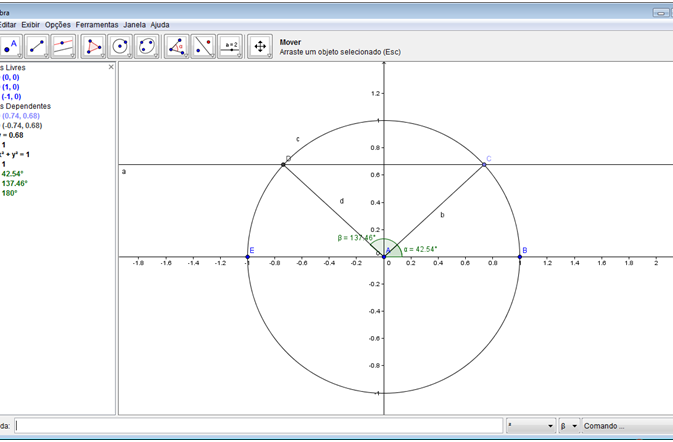
Professor, depois destes questionamentos, passe a analisar e comparar os valores do seno, cosseno e tangente dos ângulos no primeiro e segundo quadrantes. Vamos começar com o seno.
Passo 11: Criar um ponto F na intersecção do eixo y e a reta “a”. No segundo botão da barra de botões, selecione a ferramenta “Novo ponto” e clique no ponto de intersecção do eixo y e a reta “a”.
Passo 12: Criar segmento de reta ligando os pontos A e F. Para realçar este segmento, clique com o botão direito do mouse sobre o segmento criado e selecione “Propriedades”. Na aba “Cor” selecione uma cor diferente. Na aba “Estilo” altere a espessura da linha. Movimente o ponto C, observe o que acontece.
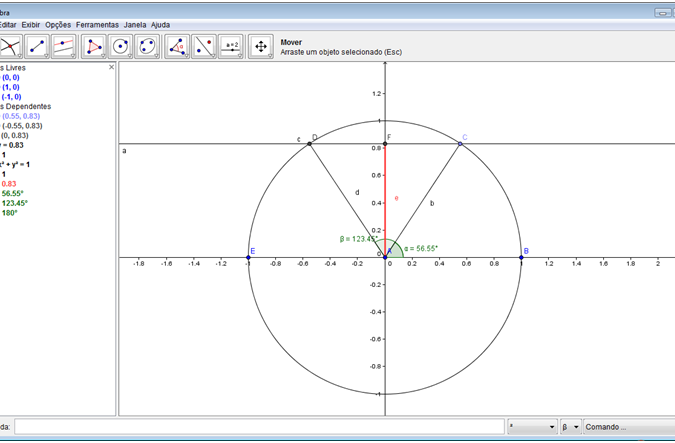
Professor questione aos seus alunos, quanto ao seno dos ângulos:
• O sen o de um ângulo é medido no eixo x ou no eixo y?
• O segmento AF representa o valor do seno do ângulo BAC?
• O segmento AF representa o valor do seno do ângulo BAD?
• Observe o valor das ordenadas dos pontos C e D. São iguais?
Vamos analisar agora o cosseno dos ângulos.
Passo 13: Criar uma reta perp endicular a reta “a” e que passe pelo ponto C. No quarto botão da barra de botões, selecione a ferramenta “Reta perpendicular” e clique na reta “a” e em seguida no ponto C.
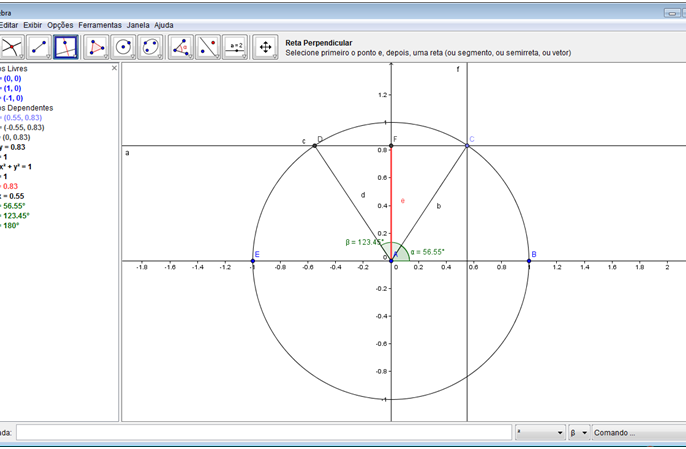
Passo 14: Crie um ponto G na intersecção do eixo x e com a reta “f”, a perpendicular criada.
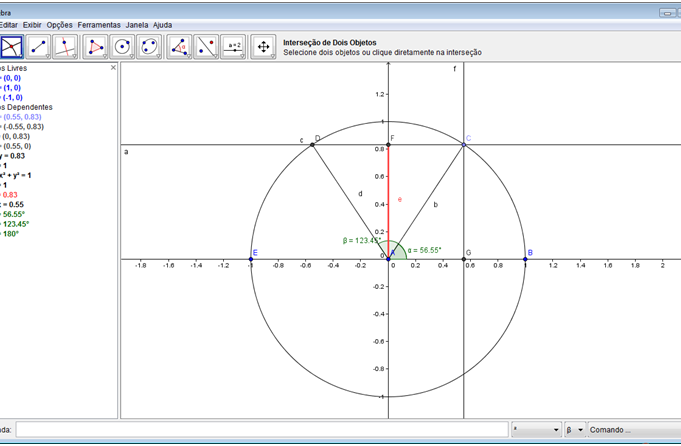
Passo 15: Criar segmento de reta ligando os pontos A e G e realce de forma diferente do segmento “e”.
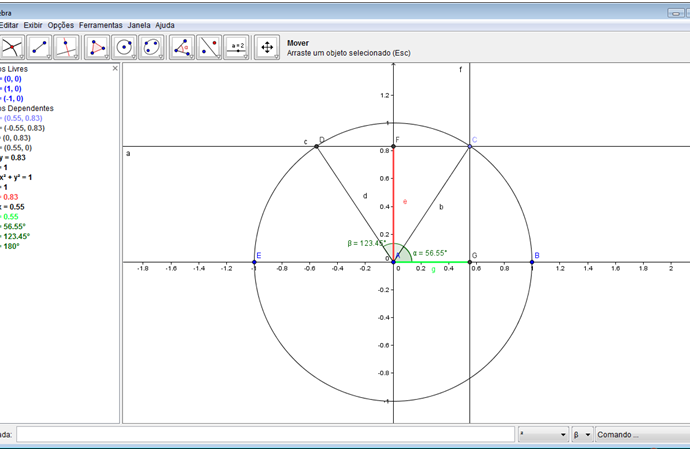
Passo 16: Criar uma reta perpendicular à reta “a” e que passe pelo ponto D. Criar um ponto de intersecção da reta criada com o eixo x e, em seguida, criar um seguimento de reta ligando o ponto A ao ponto criado. Realce o seguimento criado com as mesmas características do seguido do passo 15.
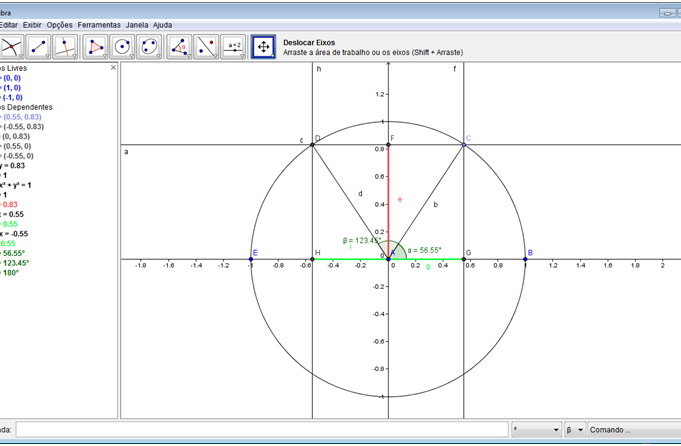
Professor questione aos seus alunos, quanto ao cosseno dos ângulos:
• O cosseno de um ângulo é medido no eixo x ou no eixo y?
• O segmento AG representa o valor do cosseno do ângulo BAC?
• O segmento AH representa o valor do cosseno do ângulo BAD?
• Observe o valor das abscissas dos pontos C e D. São iguais?
Vamos analisar agora a tangente dos ângulos.
Passo 17: Criar uma reta perpendicular à reta “a” e que passe pelo ponto B.
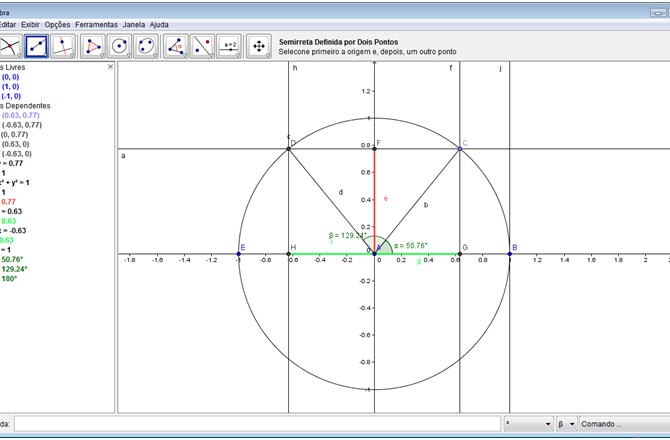
Passo 18: Criar uma semirreta ligando o ponto A ao ponto C. No terceiro botão da barra de botões, selecione a opção “Semirreta Definida por Dois Pontos”, e em seguida, clique nos pontos A e C, nesta sequência.
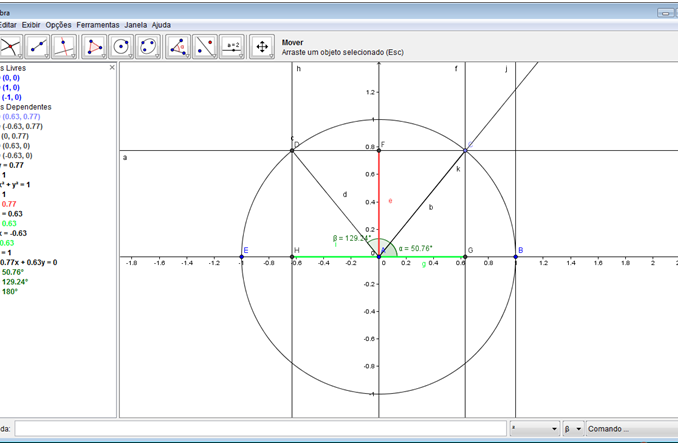
Passo 19: Criar um ponto na intersecção da semirreta c riada e a reta “j”, criada no passo 17. Em seguida, criar um segmento de reta que liga o ponto B ao ponto criado. Realce este seguimento de forma diferente dos outros criados.
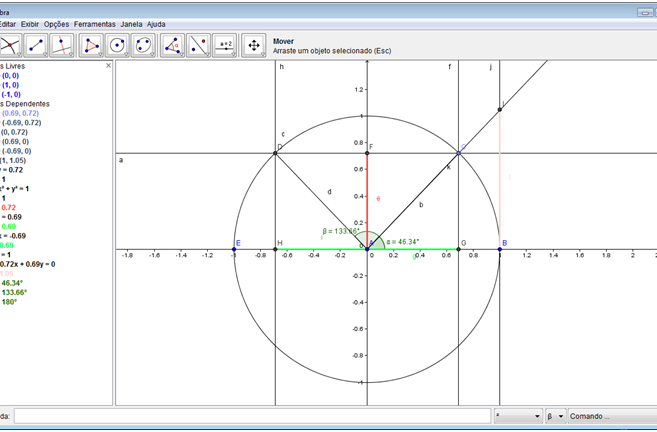
Passo 20: Criar uma semirreta ligando o ponto D ao ponto A, nesta sequência. Criar um ponto de intersecção da semirreta criada com a reta “j”, criada no passo 17. Criar um segmento de reta ligando o ponto criado ao ponto B. Realce este seguimento da mesma forma que foi realçado o seguimento do passo 18.
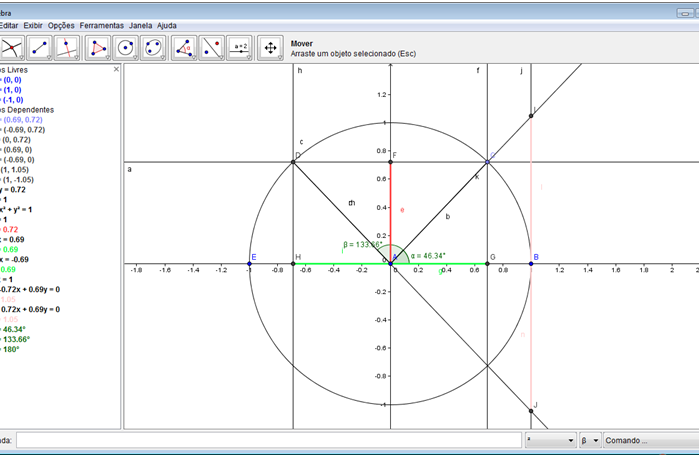
Professor questione aos seus alunos, quanto à tangente dos ângulos:
• A tangente de um ângulo é medida no eixo x, no eixo y ou em um eixo auxiliar?
• O segmento BI representa o valor da tangente do ângulo BAC?
• O segmento BJ representa o valor da tangente do ângulo BAD?
• Observe o valor das ordenadas dos pontos I e J. São iguais?
Professor, fizemos até aqui todo o detalhamento de como trabalhar a “Redução do 2º quadrante para o 1º”. Peça a eles que salvem atividade feita e, em seguida, façam a analise da “Redução do 3º quadrante para o 1º” e da “Redução do 4º quadrante para o 1º”. Esta análise pode ser ampliada para secante, cossecante e cotangente.
Professor, elabore uma lista de exercícios para que os alunos possam praticar um pouco. Utilize o livro didático e caso queira complementá-la, existe algumas lista disponíveis em:
• http://www.portalimpacto.com.br/docs/ImpactoGeorgeVest2008Aula10F2.pdf
• http://www.portalimpacto.com.br/docs/2008VestPimentelF2Aula08a11.pdf
Recursos Complementares
Avaliação
A avaliação (1 aula) poderá ser da seguinte forma:
• Atividades em sala.
• Listas de exercícios envolvendo aplicações do assunto no cotidiano.
• Durante as aulas observando o interesse e a participação do aluno.
• Estimular os alunos a criarem e participarem de Blogs sobre o assunto. Caso queira utilizar algum Blog já existente, sugerimos os seguintes:
o http://br.answers.yahoo.com/question/index?qid=20070419203143AA7ZdWl
o http://22amatematica.blogspot.com/2007/05/reduo-ao-1-quadrante.html
• Competição entre grupos, de no máximo quatro alunos, onde cada grupo apresenta um problema outro grupo caso consiga resolvê-lo, continua na competição, caso erre, será eliminado.
Quatro estrelas 3 classificações
- Cinco estrelas 2/3 - 66.67%
- Quatro estrelas 1/3 - 33.33%
- Três estrelas 0/3 - 0%
- Duas estrelas 0/3 - 0%
- Uma estrela 0/3 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Bruno Rocha, Esc particular , Bahia - disse:
bsr999@hotmail.com20/01/2015
Cinco estrelasótima utilização do Geogebra. Parabéns pela aula, está muito bem estruturada. Vou utilizar a ideia nas minhas aulas
-
Mirian, UFMT , Mato Grosso - disse:
miria_rafaela@hotmail.com09/03/2014
Quatro estrelasMuito bom, sou estudante de licenciatura e tenho que preparar algumas aulas, esse material me ajudou muito. Obrigada!.
-
Mônica Balduino de Abreu, SEEDUC , Rio de Janeiro - disse:
monicababreu@gmail.com30/10/2011
Cinco estrelasMuito Boa!! Com o uso do Geogebra melhor. Muito bem elaborada, usarei em minhas aulas.
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus


