Utilizar o conhecimento geométrico para realizar a leitura e a representação da realidade e agir sobre ela, conforme competência de área 2 da Matriz de Referência de Matemática e suas Tecnologias do ENEM.

Identificar características de figuras planas ou espaciais, conforme habilidade H7da Matriz de Referência de Matemática e suas Tecnologias do ENEM.

3 horas/aulas de 50 minutos

• Figuras geométricas e suas formas planas e espaciais;
• medida de ângulos notáveis;
• diferença entre círculo e  circunferência, raio e diâmetro.

PRIMEIRO MOMENTO: Aguçar o olhar geométrico por meio da arte.

Inicie a aula apresentando aos seus alunos a seleção de obras a seguir (figura 1). Elas são do artista e fotógrafo turco Sakir Gökcebag.

Comentário: Use o projetor multimídia para ampliar as imagens. Desse modo, o aluno poderá contemplar mais facilmente as obras e observar suas características. Para acessar o site do artista use o link: <http://www.sakirgokcebag.com/PhotoPojects.aspx>.

Figura 1: Imagens dos quadros de Sakir Gökcebag/ WM

Fonte: Adaptado de <http://www.sakirgokcebag.com/PhotoPojects.aspx>. Acesso em 18/06/2013.

Incentive seus alunos a observarem os quadros de Sakir Gökcebag ajudando-os a estabelecerem relações com as formas geométricas: quadrado, círculo, retângulo, esfera. Para isso, sugiro que durante a apresentação das obras provoque um debate com perguntas do tipo:

a) Qual é a relação dos quadros com a matemática?

b) Quais formatos as melancias utilizadas pelo artista apresentavam antes dos cortes?

c) O que você pode afirmar sobre as medidas dos ângulos usados nos cortes? 

d) Que recursos matemáticos o artista usou para produzir encaixes tão perfeitos?

e) Que figuras geométricas planas você identifica nas obras? Desenhe.

f) Que figuras geométricas espaciais você identifica nas obras? Desenhe.

Observação: Dentre as colocações dos alunos, espera-se que percebam na geometria dos quadros: formas arredondadas, esféricas, prismas, quadrados, retângulos, setor circular, as simetrias, ângulos de corte iguais a 90° e 180°.

Comentário: É importante que o professor observe se os alunos distinguem as figuras espaciais das planas. Caso seja necessário, faça uma revisão: formas bidimensionais e tridimensionais.

 

SEGUNDO MOMENTO: Construir o conceito de esfera.

Os quadros de Sakir Gökcebag chamam a atenção, entre outras coisas, para o formato esférico das melancias.  Dessa forma, este é um bom momento para trabalhar o conceito de esfera. Assim sendo, pode-se desenvolver as seguintes atividades:

1) Peça aos seus alunos que façam um esboço de uma melancia “redonda” usando o compasso. Lembre-os que estão desenhando no plano uma figura espacial, portanto precisam usar algum recurso de ilusão de ótica. Questione como isso pode ser feito e se for necessário sugira o traço equatorial para um desenho em perspectiva. Veja o modelo na figura 2.

Figura 2: representação geométrica da melancia, em perspectiva.

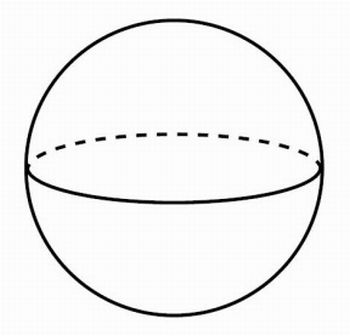
Fonte: Disponível em: <http://wchaverri.wordpress.com/formas/esfera/> Acesso em: 17 jun 2013.

2) Levante as questões, a seguir, permitindo que seus alunos falem de suas percepções.

a) Quais outros objetos do nosso cotidiano apresentam forma semelhante?

b) A forma representada é bidimensional ou tridimensional? Plana ou espacial?

c) Para construir a circunferência utilizada no desenho, você precisou utilizar o compasso. Qual é a posição do ponto representado pela ponta seca do compasso? E no desenho em perspectiva, qual é a posição desse ponto?

d) Marque três pontos distintos na circunferência. Faça a medida da distância destes até o centro.

e) Quais as medidas encontradas? O que você observa?

Comentário: Espera-se que o aluno perceba que as distâncias são iguais.

f) O que você pode concluir a respeito das distâncias de cada ponto da circunferência até o centro?

g) Considerando o desenho em perspectiva (figura tridimensional), o que se pode dizer da distância de cada ponto dessa figura até o centro?

h) Que nome você daria para a distância entre o centro e um ponto qualquer da figura?

Comentário: Nesse momento o professor deve nomear a distância do centro à superfície como sendo o raio da esfera (R).

i) Quando inserimos a linha equatorial, a circunferência ganha uma aparência tridimensional. Você sabe qual é o nome dado a essa forma geométrica?

Comentário: É importante que as perguntas sejam escritas no quadro ou que sejam entregues aos alunos impressas, para que os mesmos possam copiar e registrar as conclusões da classe.

 

PENSE UM POUCO! ...

(A) O que diferencia uma melancia de uma bola?

Resposta esperada: Que a melancia é sólida (casca, massa branca e massa vermelha) e a bola é oca (“casca”).

(B) A melancia (redonda) utilizada pelo artista em seus quadros, pode ser comparada a uma esfera. 

Nesse caso, a esfera também pode ser comparada a uma bola? Por quê?

Resposta esperada: Não, porque como a esfera é comparada com a melancia ela não pode ser oca.

(C) Faça ou projete um desenho que ilustre a esfera (figura 3). Não se esqueça de identificar o centro e o raio da sua esfera.

Figura 3: modelo de esfera

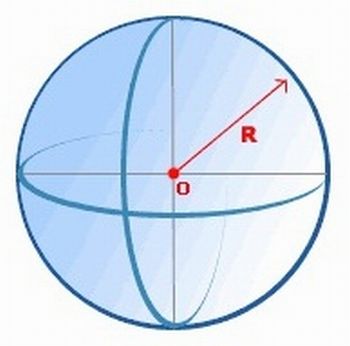
Fonte: http://www.zmaisweb.com/home/index.php/em01/90-esfera

Agora....

Construa então a definição de esfera, considerando questões como: centro, raio e distância.

Espera-se uma resposta próxima à definição formal da esfera: “Uma Esfera de centro O e raio R é o conjunto dos pontos do espaço cujas distâncias a O são menores ou iguais a R”.(SMOLE, 2003, p. 281).

Comentário: Observe com os alunos que: “a esfera é um sólido perfeito por não ter arestas e por apresentar sempre a mesma forma, qualquer que seja o ângulo de observação.”. (SMOLE, 2003, p. 281).

(D) No desenho a seguir, está representada uma esfera com dois raios alinhados, ligando uma extremidade à outra da figura e passando pelo centro da mesma (figura 4). O segmento formado por esses dois raios é chamado de diâmetro.

Figura 4: Destaque do diâmetro em uma esfera

Agora responda:

1) Como encontramos a medida do diâmetro (D) da figura 4?

Resposta esperada: “somando a medida dos raios” ou “dobrando a medida do raio”, etc.

2) Você consegue estabelecer uma relação matemática entre diâmetro (D) e raio (R)?

Resposta esperada: “D = R + R” ou “D = 2*R”.

Para finalizar esse momento, proponha aos alunos a seguinte atividade:

Atividade: “Usando o compasso,  desenhe 3 esferas em uma folha A4, de raios com medidas iguais a R=2 cm, R=3 cm e R=5 cm, respectivamente. Determine os diâmetros de cada uma de suas esferas”.

Professor, recolha a atividade para avaliar.

Comentário:Durante a atividade verifique se seus alunos estão utilizando o compasso corretamente e confira se os mesmos conseguiram fazer uma representação em perspectiva e também se estão destacando o centro e o diâmetro.

 

SEGUNDO MOMENTO: Construir a ideia de Superfície Esférica

PENSE!...

Vimos que a casca, a massa branca e a massa vermelha de uma melancia (redonda) constitui a esfera. No entanto, se considerarmos apenas a casca, o que teremos?

Professor, explore as respostas dos alunos. Para isso, levante questões que os levem a pensar nas palavras “superfície” e “esférico”.

Sugestões:

Ideia de superfície

O que você está cobrindo, por exemplo, quando:

 - reveste o tampo de uma mesa?

 - Pinta uma parede?

- Encapa um caderno?

- Azuleja o chão ou uma parede?

Ideia de “esférica”

a - Qual é a diferença entre a superfície formada pelo revestimento da mesa e a superfície formada apenas pela casca verde da melancia (redonda), utilizada pelo artista?

Comentário: Espera-se que o aluno observe que a superfície da mesa é plana, enquanto que a que reveste a melancia (casca) é “curva”.

b - Então se a melancia representa uma esfera, como pode ser chamada a sua casca?

Comentário: Aproveite as “falas” e, se  necessário, antes de definir a superfície de revestimento da esfera como “Superfície Esférica” ressalte a questão do nome da figura (esfera),

Solicite aos alunos que registrem, com suas palavras, a definição de superfície esférica. Em seguida socialize as respostas. Esteja atento para alguma modificação ou complementação nas respostas apresentadas. Registre no quadro a resposta que foi apresentada na forma mais completa.

Resposta esperada: Superfície esférica de centro O e raio R é o conjunto dos pontos do espaço cujas distâncias a O são iguais a R.(SMOLE, 2003, p. 281).

 

Terceiro Momento: A esfera é um sólido de revolução.

Enriqueça a percepção de seus alunos apresentando a eles a possibilidade de girar um semicírculo em torno do diâmetro (volte na figura anterior e identifique o diâmetro da esfera) e veja qual a figura que será visualizada. É possível uma experiência simples colando o semicírculo em uma vareta e realizando uma rotação (figura 5).

Figura 5: visualização da esfera, por meio da revolução do semicírculo

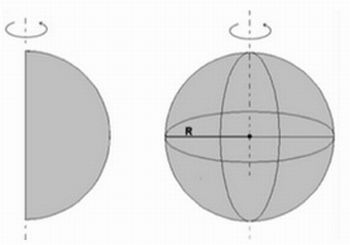
Fonte: disponível em: http://www.google.com.br/imgres?imgurl=http://1.bp.blogspot.com/

Essa atividade pode ser realizada com o uso de equipamentos eletrônicos. O aluno pode conhecer esse equipamento assistindo ao vídeo “Esfera de revolução”, disponível no site:

http://www.youtube.com/watch?v=2aO5IxM1QM0&list=UUrzp98BB0GNKrOFOhIVwNBA. Acesso em: 17 jun 2013

Proponha aos alunos a seguinte atividade:

Atividade:

1- Observando o procedimento prático utilizado na construção da esfera, é possível construir uma superfície esférica?

Espera-se que eles percebam que sim desde que tirem o “miolo”, deixando apenas a linha do semicírculo.

2- Construa uma superfície esférica.

Para essa atividade, devem estar disponíveis algumas varetas, pedaços de arame e alicate.

CURIOSIDADE...

Quando a melancia não for esférica, como mostrada na figura 6, qual é o seu formato?

Figura 6: Melancia alongada

Fonte: http://www.google.com.br/imgres?imgurl=http://trabalhandomuito.files.wordpress.com/

Peça para que pesquisem o nome do formato e uma maneira de representá-la por meio de um desenho uma forma para construí-la.

DANTE, Luiz Roberto. Matemática. São Paulo: Ática, 2005.

http://cmup.fc.up.pt/cmup/arte/

http://artenaescola.org.br/uploads/boletins/boletim-65.pdf

http://artenaescola.org.br/dvdteca/catalogo/dvd/?id_video=115

http://www.sakirgokcebag.com/PhotoPojects.aspx

SMOLE, Kátia C. S. Matemática. São Paulo: Saraiva, 2003. (ensino médio, v.2)

Além da participação nas atividades, ao avaliar os alunos, leve em consideração o processo de desenvolvimento das atividades solicitadas, tendo como critérios:

1. As discussões decorrentes das questões iniciais.

2. A atividade número 5, recolhida.

3. As respostas das questões apresentadas em todos os momentos.

4. A representação das esferas (com régua e compasso).

5. A atividade prática envolvendo a construção da superfície esférica de revolução (terceiro momento).

6. A pesquisa realizada.