08/02/2010

|

|

|

|

|

|
Antomar Araújo Ferreira, Marcia Aparecida Mendes
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Fundamental Final | Matemática | Espaço e forma |
O que o aluno poderá aprender com esta aula
- Estabelecer as relações métricas no triângulo retângulo, através da manipulação de triângulos retângulos de papel.
- Compreender as relações métricas no triângulo retângulo.
- Aplicar as relações do triângulo retângulo.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Para se fazer este estudo dirigido é necessário que se retome com o aluno:
- A classificação de triângulos quanto aos lados e quanto aos ângulos.
- Elementos do triângulo retângulo: catetos, hipotenusa e altura relativa à hipotenusa.
- Triângulos congruentes.
- Triângulos Semelhantes.
Estratégias e recursos da aula
Este assunto será desenvolvido utilizando um estudo dirigido que deverá ser feita passo a passo pelo aluno.
A aula em sua íntegra esta escrita abaixo. O que está destacado são sugestões dirigidas apenas ao professor.
Estudaremos nesta aula as Relações métricas no triângulo retângulo.
Antes de trabalhar com o aluno as relações métricas, devem-se retomar alguns conceitos importantes que serão usados neste estudo. Abaixo segue algumas sugestões de atividades:
1) Dos triângulos abaixo, colora os que são retângulos.
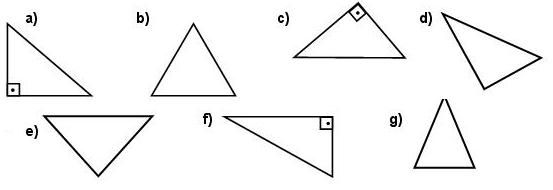
O professor deve fazer a correção, falando o mínimo possível, fazendo com que os alunos relembrem os conceitos. É necessário fazer com que os alunos recordem: a classificação dos triângulos quanto aos ângulos, dando mais ênfase ao triângulo retângulo; a classificação dos triângulos quanto aos lados; os elementos dos triângulos (lados, ângulos internos e externos); os lados do triângulo retângulo que possuem nomes especiais, etc.
2) Identifique os catetos e a hipotenusa em cada um dos triângulos:
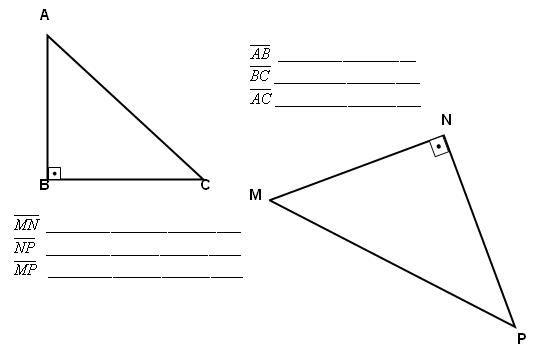
3) Observe o triângulo abaixo e escreva abaixo de cada segmento o seu respectivo nome, utilizando as palavras “cateto, hipotenusa, altura relativa à hipotenusa, Projeção de AM e Projeto de MT sobre a hipotenusa”:
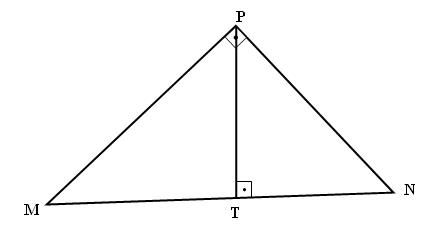

4) Na malha abaixo destaque, utilizando cores, os pares de triângulos semelhantes.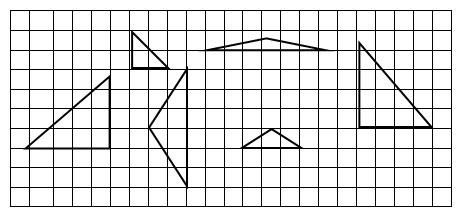
Após retomar todos esses conceitos através da interatividade e da participação ativa dos alunos, comece, então, a partir de agora a desenvolver o estudo dirigido sobre as Relações Métricas no Triângulo Retângulo.
Este estudo digirido quando trablhado em duplas produz maior aproveitamento, pois há a troca de informações e ajuda mútua no momento de manipulação dos triângulos que serão recortados. A interferência do professor deve ser mínima, ou nenhuma se possível. É muito enriquecedor se as dúvidas que surgirem forem compartilhadas entre as próprias duplas, antes da intervenção do professor.
Para conhecer as relações métricas no triângulo retângulo, nada melhor, do que vocês mesmo descobrirem-nas. Para isso, faça o que é proposto:
Considere o triângulo ABC abaixo, retângulo em A e complete:
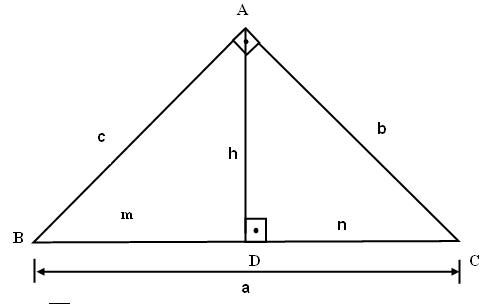
- O lado AC, de medida b, denomina-se _______________________.
- O lado AB, de medida c, denomina-se ________________________.
- O lado BC, medida a, denomina-se ________________________.
- O segmento AD, de medida h é a _______________________ do triângulo ABC, relativa à hipotenusa BC.
- O segmento BD, de medida m, é a projeção ortogonal do _________________ sobre a hipotenusa.
- O segmento DC de medida n é a projeção ortogonal do __________________ sobre a _________________.
- O segmento AD divide o triângulo ABC em dois triângulos. São eles, Triângulo ______ e Triângulo ____ __.
Vamos descobrir a relação entre o triângulo original ABC e os triângulos ABD e ACD, obtidos ao traçar o segmento AD.
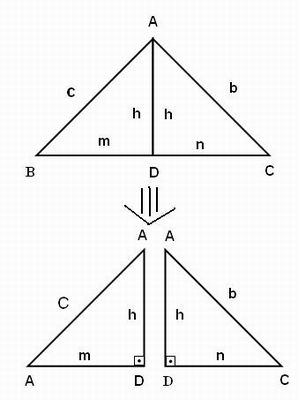
Para isso façam o que é proposto:
1) Recorte os dois triângulos desenhados na última folha.
O professor deve fornecer os triângulos que constam do anexo 1 para cada aluno. Se preferir pode fornecer triângulos maiores.
Compare os triângulos que você recortou. Esses dois triângulos são congruentes ou semelhantes? Por quê?
2) Pegue o triângulo I e recorte-o de modo a obter os triângulos ABD e ACD.
3) Dos triângulos obtidos, pegue o triângulo ABD e compare-o com o triângulo II, sobrepondo-os de modo que os ângulos congruentes coincidam e que os catetos e a hipotenusa se correspondam.
Nesse momento o professor deve-se orientar a cada dupla que na sobreposição, o ângulo reto do triângulo ABD fica sobre o ângulo reto do triângulo ABC e que cada ângulo agudo corresponde ao ângulo agudo do outro.Esses triângulos que você acaba de comparar, são congruentes ou semelhantes? Justifique.
4) Agora pegue o triângulo ACD obtido e compare-o com o triângulo II e sobreponha-os da mesma maneira que no item anterior, ou seja, de maneira que os ângulos congruentes coincidam e que os catetos e a hipotenusa se correspondam.
Esses dois triângulos também são semelhantes? Por quê?
5) E por último, pegue os dois triângulos ABD e ACD obtidos com o recorte, sobreponha-os de modo que os ângulos congruentes coincidam e que os catetos e a hipotenusa se correspondam. Eles serão semelhantes ou congruentes? Por quê?
Já que acabamos de constatar que os pares de triângulos que comparamos, são semelhantes sabemos então que seus lados são proporcionais. Passemos, então para a etapa de obtenção das relações métricas.
Nessa etapa você terá que sobrepor novamente cada par de triângulos semelhantes citados em cada item anterior, verificando os elementos correspondentes para, a seguir, completar as proporções indicadas resolvendo o que for possível para chegar à relação métrica.
1ª relação:
Δ ABC ~ Δ DAB (não se esqueça que no ABC temos que a = m+n)
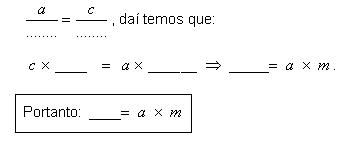
É uma relação métrica no triângulo retângulo. Escrevendo por extenso, temos:
Quadrado da medida c do cateto = medida da hipotenusa X medida da projeção deste cateto.
Desafio:
Coloque um exemplo de aplicação como desafio. Peça a dupla que terminar primeiro e corretamente para resolvê-lo explicando para as demais.
2ª relação:
Δ ABC ~ Δ DAC
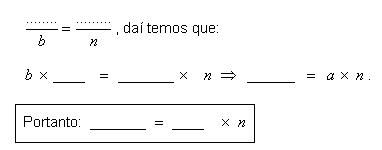
É outra relação métrica no triângulo retângulo. Escrevendo por extenso, temos:
Quadrado da medida b do cateto = medida da hipotenusa X medida da projeção deste cateto.
Desafio:
Coloque um exemplo de aplicação como desafio, solicitando a dupla que terminar em primeiro lugar e corretamente para resolvê-lo explicando para as demais.
3ª relação:
Δ ABD ~ Δ CAD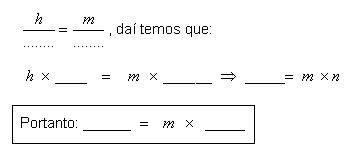
É mais uma relação métrica no triângulo retângulo. Escrevendo por extenso, temos:
Quadrado da medida h do cateto = medida da projeção do cateto de medida c X medida da projeção do cateto de medida b.
Desafio:Vimos então que no triângulo retângulo são válidas as relações:
I) b2 = ___________.
II) c2 = ___________.
III) h2 = ___________.
Agora, a partir dessas relações, obtenha duas outras novas relações.
1ª) Multiplique membro a membro as relações I e II, ou seja, multiplique o primeiro membro da relação I, pelo primeiro membro da relação II e o segundo membro da relação I pelo segundo membro da relação II, assim:
b2 x _____ = a x m x ___ x n efetuando o que é possível temos:
b2 x c2 = _____ x m x n ( A )
Como temos a relação h2 = m x n, substituindo na igualdade ( A ) acima, obtemos:
b2 x c2 = a2 x ________ ( B )
Extraindo a raiz quadrada dos dois membros da igualdade ( B ) acima, temos a relação métrica: b x ____ = a x ____ .
Escrevendo por extenso, temos:
Medida b do cateto x medida c do cateto = medida da hipotenusa x medida da altura.
Desafio:
Coloque um exemplo de aplicação como desafio, solicitando a dupla que terminar primeiro e corretamente para resolvê-lo explicando para as demais.2ª) Para conseguirmos esta última relação métrica adicione membro a membro as relações I e II, ou seja, some o primeiro membro da relação I com o primeiro membro da relação II e o segundo membro da relação I com o segundo membro da relação II, assim:
b2 + c2 = a x m + _____ (fatorando o segundo membro, coloque o a em evidência)
b2 + c2 = a x (______) ( C )
Como sabemos que a soma das medidas das duas projeções dos catetos sobre a hipotenusa no triângulo retângulo é igual a medida da hipotenusa, ou seja, no nosso triângulo original temos m + n = a e substituindo m + n = a na igualdade (C) acima, obtemos:
b2 + c2 = a x __ .
Efetuando a potenciação no segundo membro, finalmente obtemos:
b2 + ____ = _____
Esta relação métrica é chamada de TEOREMA DE PITÁGORAS. Escrevendo-a por extenso, temos:
Quadrado da medida b do cateto + quadrado da medida c do cateto = Quadrado da medida da hipotenusa.
Desafio:
Coloque um exemplo de aplicação como desafio, solicitando a dupla que terminar primeiro e corretamente para resolvê-lo explicando para as demais.
Solicite aos alunos que façam uma síntese do que foi visto, escrevendo todas as relações métricas obtidas.Retomando o início desse estudo, temos:
- a é a medida da ______________________________.
- h é a medida da _______________ _______________.
- m é a medida da _____________________________.
- n é a medida da ______________________________.
- b e c são medidas dos __________________________.
Concluindo:
Em qualquer triângulo retângulo temos:
a) O quadrado de cada cateto é igual ao produto da __________________ pela sua projeção sobre a hipotenusa.
b) O quadrado da altura é igual ao produto das ______________________ dos catetos sobre a hipotenusa.
c) O produto dos catetos é igual ao produto da ___________________________ pela ___________________.
d) O quadrado da _____ _______________________ é igual à soma dos quadrados dos _________________________
No quadro abaixo, a primeira coluna apresenta a proposta de exercício e a terceira coluna apresenta as respostas que não obedecem a mesma ordem do que foi proposto. Resolva o exercício na coluna do meio e associe à resposta correspondente na última coluna.
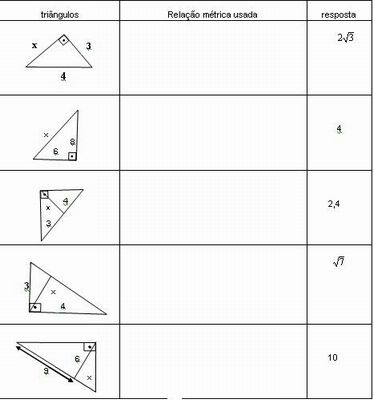
Depois que todos os alunos terminarem o professor faz a troca das folhas entre as duplas para que cada uma verifique como foi a resolução da outra. Podem surgir resoluções diferentes e essa troca faz com que a aprendizagem seja mais dinâmica.
A seguir apresentamos os moldes de triângulos que o professor deve fornecer para os alunos. Neles as letras que representam as medidas e os vértices estão repetidas, dentro e fora do triângulo, pois os triângulos serão recortados. O triângulo I é o que tem que ser recortado para obter os triângulos ABD e ACD.
Triângulo I
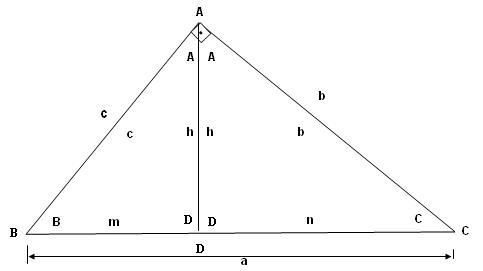
Triângulo II
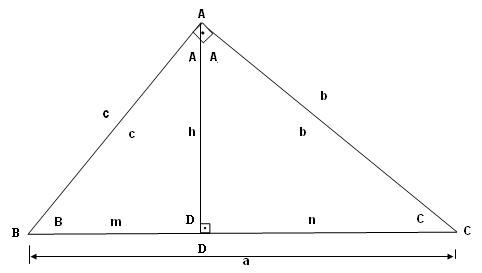
Recursos Complementares
http://www.portalimpacto.com.br/docs/01JerleyF32ANOAula02RelacoesMetricasnoTrianguloRetangulo2.pdf
http://www.unesp.br/prograd/PDFNE2004/artigos/eixo10/oteoremadepitagoras.pdf
Avaliação
A avaliação será feita durante todo o estudo dirigido através de observação da participação dos alunos, através também dos desafios propostos e finalmente com a última atividade que deverá ser trocada entre as duplas.
Quatro estrelas 3 classificações
- Cinco estrelas 2/3 - 66.67%
- Quatro estrelas 0/3 - 0%
- Três estrelas 1/3 - 33.33%
- Duas estrelas 0/3 - 0%
- Uma estrela 0/3 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
wallace chagas, wallace chagas , Rio de Janeiro - disse:
crcfoavr@yahoo.com.br19/04/2012
Cinco estrelasPara mim foi otimo
-
LENYCE, ESTADUAL , Goiás - disse:
NYCEGARCIA@HOTMAIL.COM13/07/2011
Três estrelasDEVERIA TER 1 LUGAR ONDE PUDESSEMOS TIRAR NOSSAS DUVIDAS.
-
Rodrigo Marques de Souza, COLEGIO CECILIA MEIRELES , Bahia - disse:
rodrigopiritiba@yahoo.com.br16/08/2010
Cinco estrelasGostei muito da aula o desenvolvimento é estimulante e os alunos adoraram. Parabéns!!! E obrigado pela dica.
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus

