Portal do Professor

Portal do Governo Brasileiro

CADASTRE-SE

ESQUECEU SUA SENHA?

Início do Conteúdo

VISUALIZAR AULA

Esfera

03/01/2012

Autor e Coautor(es)

Autor: Lutécia Gasparoto

CURITIBA - PR SANTO AGOSTINHO C E E FUND MEDIO

Coautor(es):

Marcos Paim, Eziquiel Menta

Estrutura Curricular

Modalidade / Nível de Ensino	Componente Curricular	Tema
Ensino Fundamental Final	Matemática	Espaço e forma
Ensino Médio	Matemática	Geometria

Dados da Aula

O que o aluno poderá aprender com esta aula

Noções e definições envolvendo a esfera. Explorar o sólido em 3D com o apoio do software de apresentação Impress/BrOffice.

Duração das atividades

2 aulas de 50 minutos.

Conhecimentos prévios trabalhados pelo professor com o aluno

Conceitos de ângulo, diâmetro, raio e medidas. Noções de plano cartesiano.

Estratégias e recursos da aula

A esfera é um importante sólido da geometria. Além disso aparece em inúmeras aplicações importantes da vida cotidiana. Nessa aula também apresentamos uma forma de manipular o sólido em 3D usando o programa de apresentações do BrOffice, o Impress ( http://www.broffice.org ).

Abaixo uma imagem da esfera que o professor pode apresentar aos alunos.

Recurso disponível em: http://pt.wikipedia.org/wiki/Esfera

Sempre que possível, é importante relacionar conteúdos com a vida cotidiana. Eis um exemplo que pode ser usado. Não deixe de ver a animação.

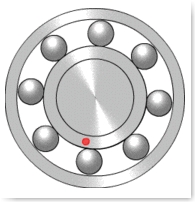
Fonte e Animação:http://pt.wikipedia.org/wiki/Rolamento

Os rolamentos são formados por esferas que permitem que ocorra o giro de uma roda em um eixo, como por exemplo nas rodas dos carros.

Sugerimos que o professor proponha que os alunos conheçam melhor a esfera por meio da criação das suas próprias esferas.

Para isso o BrOffice/Impress ( http://www.broffice.org ) oferece um excelente recurso de desenho de objetos em 3D. Vamos ver como isso pode ser feito. É simples.

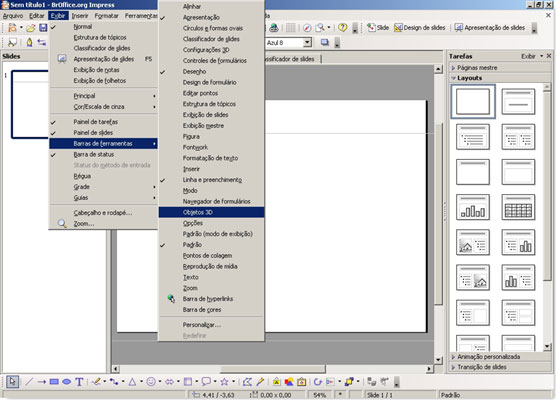
O primeiro passo é exibir a barra de ferramentas de desenho para objetos em 3D.
Basta seguir o caminho indicado na figura acima: Exibir > Barra de ferramentas > Objetos 3D
Clicando no ícone da esfera pode-se desenhar, girar, redimensionar e alterar a cor da esfera em 3 dimensões.
Observe o exemplo abaixo:

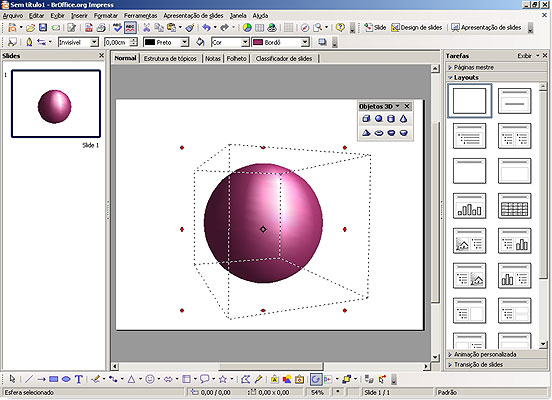
Uma vez que os alunos tenham tido a oportunidade de manipular e conhecer um pouco mais sobre a esfera, pode-se partir para um aprofundamento do estudo da esfera.

Definição de uma esfera
Uma esfera é definida como um sólido de centro O e raio R cujos conjunto de pontos do espaço estão a uma distância do centro igual ou menor que R. Eis uma ilustração a ser apresentada aos alunos:

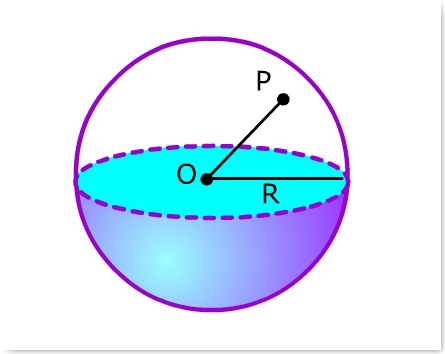
Fonte: imagem cedida pelo autor.

Área e Volume de uma Esfera

Considerando as interações anteriores, é possível partir para os cálculos mais comuns envolvendo esferas, que são a determinação da área e do volume. O professor pode propor alguns desafios para que sejam utilizadas as expressões abaixo.

Área
A área de uma esfera pode ser obtida a partir da expressão:

A = 4 . 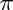. R²

Volume
O volume da esfera é dado pela expressão:

V = 4 . 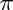. R³
3

Com os recursos apresentados até aqui é possível partir para um trabalho que envolva a aplicação do que foi estudado. O professor pode pedir aos alunos que procurem outras aplicações da esfera na vida cotidiana e também realizar cálculos de área e volume. Se possível, a continuidade do trabalho com o programa de apresentações Impress nesse conteúdo poderia tornar a aula mais interessante aos alunos.

Recursos Complementares

Também pode-se trabalhar com os aluno a criação de um mapa conceitual, no papel ou no computador (http://pt.wikipedia.org/wiki/Mapa_conceitual). Integrar no mapa outros sólidos da geometria espacial além das aplicações da esfera permitirá aos alunos construir relações mais elaboradas da geometria e suas aplicações.

Avaliação

Como forma de avaliação o professor pode solicitar aos alunos que elaborem uma apresentação no programa Impress/BrOffice sobre a esfera e realizem uma apresentação aos colegas, compartilhando e discutindo o que foi aprendido. Também é importante avaliar o desempenho dos alunos durante os trabalhos, pedindo aos alunos que revezem as posições e fazendo intervenções no processo, buscando ajudar os alunos que possuam eventuais dificuldades com o conteúdo.

Opinião de quem acessou

Três estrelas 6 classificações

Cinco estrelas 1/6 - 16.67%
Quatro estrelas 3/6 - 50%
Três estrelas 2/6 - 33.33%
Duas estrelas 0/6 - 0%
Uma estrela 0/6 - 0%

Denuncie opiniões ou materiais indevidos!

Opiniões

cristiane , ufscar , São Paulo - disse:
cristianefurriel@msn.com
12/09/2013
Três estrelas
Gostei da aula, pois utilizou animação facilitando o entendimento e despertando a curiosidade. Apenas as formulas que foram passada de forma muito direta.

Andre, Particular , Rio de Janeiro - disse:
cardeal213@bol.com.br
12/08/2013
Cinco estrelas
Muito bom.

Rayane, Escola Coronel Jose Pinto de Abreu , Pernambuco - disse:
rayanepaulinno@hotmail.com
08/06/2012
Três estrelas
Bonzinho *---*

Cristiane Fernandes Dimer Carlos, INSTITUTO ESTADUAL DE EDUCAÇÃO MARIA ANGELINA MAGGI , Rio Grande do Sul - disse:
cristianedimer@gmail.com
24/03/2010
Quatro estrelas
Muito interessante a aula desenvolvida, pois além de ter definições possuem desenhos que ilustram e possibilitam uma melhor compreensão sobre o conteúdo estudado.

Francisco Carlos Morreira Martins, COLEGIO ESTADUAL PAULO SARASATE , Ceará - disse:
carloskorigão@yahoo.com.br
24/03/2010
Quatro estrelas
Muito boa a aula elaborada, por causa de ter varias formas ainda possuem inlustrações que possibilitam um melhor rendimento sobre o conteúdo estudado.

Inaldo Lopes de Andrade, SECRETARIA MUNICIPAL DE EDUCAÇÃO DE JOÃO PESSOA , Paraíba - disse:
inaldolopes1@hotmail.com
24/03/2010
Quatro estrelas
O projeto de aula é muito bom, possibilita a interação do aluno com o computador e com os sites da internet, facilitando o entendimento do conceito de esfera e o cálculo de sua área e volume.