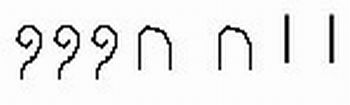16/12/2010
Eziquiel Menta
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Educação de Jovens e Adultos - 2º ciclo | Matemática | Grandezas e medidas |
| Ensino Médio | Matemática | Números e operações |
| Educação Escolar Indígena | História | Modos de viver |
| Ensino Médio | História | Processo histórico: nações e nacionalidades |
O que o aluno poderá aprender com esta aula
§ Reconhecer elementos que compõe o sistema de numeração egípcio.
§ Operar com diferentes sistemas de numeração com o intuito de desenvolver novas leituras e compreensões da matemática.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Conhecimentos de matemática básica.
História do civilização egípcia.
Estratégias e recursos da aula
Para iniciar essa aula, sugere-se a antecipadamente trabalhar os conteúdos previstos na aula História dos números naturais: onde e como surgiu? Disponível em: http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=22107, acesso em 08 de novembro de 2010.
Após a realização da aula sugerida, explicar aos alunos que o foco dado neste momento será aos processos que envolvem o Sistema de Numeração dos Egipcios.
Atividade 1
No laboratório de informática, com os alunos reunidos em grupos (3 a 4 alunos), propor a realização das atividades do recurso Egipto, disponível em: http://nautilus.fis.uc.pt/mn/egipcia/index.html, acesso em 08 de novembro de 2010.
Para a atividade, o professor deve propor que os grupos procurem descobrir quais simbolos equivalem aos números apresentados nas atividades do recurso. Para isso podem contar apenas com a ferramenta Ajuda. A medida que forem fazendo descobertas, que anotem no caderno suas observações. Permita que os alunos realizem a atividade durante uns 20 minutos.
Fonte: http://nautilus.fis.uc.pt/mn/egipcia/index.html
Ainda com os alunos nos grupos, explique que durante muito tempo, o campo mais rico da História da Matemática repousou no Egito. Que a maior parte dos nossos conhecimentos sobre a matemática egípcia deriva de dois papiros: O Papiro de Rhind, que contém 85 problemas, e o chamado Papiro de Moscovo, talvez dois séculos mais antigo, que contém 25 problemas. O papiro é uma planta originária do Egito. Eles se aproveitavam das suas folhas umedecidas e as colocavam para secar sobre tábuas. Dessa forma, obtinham longos rolos onde faziam registros. Os mais notáveis aparecem nos túmulos egípcios.
|
Em 1858, A. Henry Rhind um jovem antiquário escocês, adquiriu um papiro muito antigo. Um rolo de uns 5,5 metros de comprimento por 33 cm de largura, mas estava desfeito aos pedaços e faltavam alguns fragmentos, quando chegou às mãos do antiquário. Alguns destes fragmentos apareceram, meio século mais tarde nos arquivos da Historic Society, de Nova York. Tinham sido obtidos pelo colecionador Edwin Smith.O Papiro de Rhind foi adquirido, após a morte deste, pelo British Museum, onde se conserva até hoje. O rolo consiste num manual prático de matemática egípcia, escrito por volta dos anos 1700 a.C. e é a principal fonte de conhecimentos acerca de como contavam, calculavam e mediam os egípcios. Foi escrito por um escriba chamado Ahmés. O papiro de Rhind contém 85 problemas. Mostra o uso de frações, a resolução de equações simples e de progressões, a medição de áreas de triângulos, trapézios e retângulos, o cálculo de volumes de cilindros e prismas, etc. Das indicações dadas pelo papiro de Rhind, inferimos que os geómetras egípcios atribuíam ao número pi um valor equivalente ao quadrado da fração 16/9 que daria, em número decimal, 3,1605, valor no qual o pi apresenta um erro que não chega a dois centésimos da unidade!!
Fonte: http://www.educ.fc.ul.pt/icm/icm99/icm36/papiro_de_rhind.htm, acesso em 08 de novembro de 2010. |
| Também conhecido como papiro Golenischev, o Papiro de Moscovo é quase tão comprido como o papiro de Rhind, mas com apenas uns sete centímetros de largura. Foi escrito por um escriba desconhecido da dinastia XII (1890 a.C.) e foi comprado no Egito no ano 1893, conservando-se até hoje em Moscovo, daí o seu nome. Trata-se de uma coleção de 25 problemas resolvidos, sobre questões do quotidiano. Fonte: http://www.educ.fc.ul.pt/icm/icm99/icm36/papirode.htm, acesso em 08 de novembro de 2010. |
O sistema de numeração proposto pelos Egípcios é bastante interessante e baseia-se em agrupamentos. Professor, a medida que for explicando, permita que os alunos se manifestem, apresentando as observações que anotaram da atividade 1.
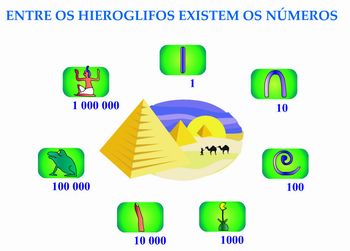
Neste sistema, os números são representados por símbolos especiais para 1, 10, 100, 1000 e de uma forma aditiva: 1 era representado por uma marca que se parecia com um bastão |; 2 era representado por duas marcas ||; E assim por diante...
Quando chegavam a 10, eles trocavam as marcas por um "U invertido" e assim continuavam até o 19.
Depois, o 20 era representado por dois "U invertido". O 30 por três e assim sucessivamente.
Para registar 100, em vez de utilizar o "U invertido", trocaram este agrupamento por um novo símbolo, que parecia um pedaço de corda enrolada. Juntando vários símbolos de cem, escreviam o 200, 300, ..., 900. Dez marcas de 100 foram substituídas por um novo símbolo, a figura da flor de lótus. E, trocando cada dez marcas iguais por uma nova, eles escreveram todos os números de que necessitavam.
Fonte das imagens: http://www.educ.fc.ul.pt/icm/icm99/icm36/numeracao_egipcia.htm, acesso em 08 de novembro de 2010.
Obs. Clique sobre as imagens para vê-las em tamanho ampliado.
Com todos estes símbolos criaram um sistema de numeração de base decimal não posicional, isto é, com agrupamentos de unidades, dezenas, centenas, etc. de forma semelhante ao que nós fazemos. Por exemplo, para escrever 1234, eles juntariam quatro símbolos de unidades, três de dezenas, dois de centenas e um de milhar.
Porém, essa ordem poderia ser inversa, e por isso dizemos que o sistema em questão não era posicional.
| Observe como eles escreviam o número 322: |
100 + 100 + 100 + 10 + 10 + 1 + 1 da mesma forma, poderia ser 1 + 1 + 10 + 10 + 100 + 100 + 100 dando o mesmo resultado. |
Atividade 2
Com os alunos em sala de aula (ainda reunidos em grupos), propor as seguintes problemáticas:
a) Escrever os seguintes números a partir dos sistema de numeração egipcio.
- 23
- 4562
- 103562
Resolução:
Fonte: http://www.educ.fc.ul.pt/icm/icm99/icm36/solucoes.htm#Numeração Egípcia, acesso em 08 de novembro de 2010.
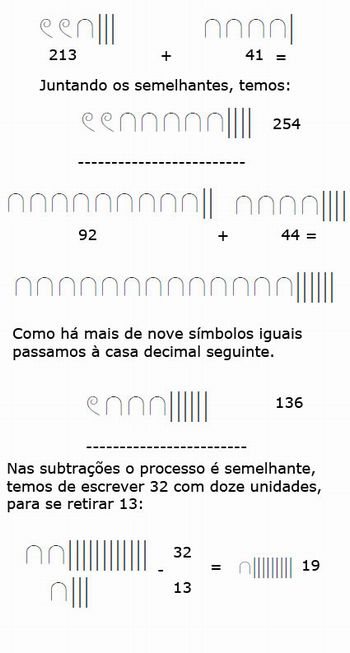
b) Utilizando o sistema de numeração egipcio, efetuar as seguintes operações:
213+41 =
92 + 44 =
32 - 13 =
Resolução:
Fonte: a autora.
Atividade 3
Propor aos alunos a atividade de pesquisa orientada conforme sugere a WebQuest* A Matemática e a Civilização Egípcia, que têm por objetivo propiciar aos alunos perceber a relação existente entre o Povos do Egito e o conhecimento de Matemática, disponível em: http://www.webquestbrasil.org/criador/webquest/soporte_tablon_w.php?id_actividad=6295&id_pagina=1, acesso em 08 de novembro de 2010.
Ao final da atividade de pesquisa, os alunos deverão produzir um texto apresentando as aproximações que perceberam entre o conhecimento matemático e as contríbuições da civilização egípcia, além de outros conhecimentos que apreenderam durante a realização da pesquisa e da aula. Após a pesquisa, propor uma rodada entre os grupos para socializar as produções.
Lembrando que a WebQuest é uma metodologia de pesquisa online, organizada por meio de um roteiro que segue com os seguintes passos: introdução, tarefa, recursos, processo, avaliação, conclusão. O professor dá indicativos de sítios, pré-selecionados, para que a aula seja aproveitada ao máximo, e os alunos não se distraiam diante de tantas informações da internet, e organizem a tarefa e a concluam com sucesso.
Proposta Interdisciplinar:
1 - Se o professor julgar necessário, pode ainda propor o vídeo Nossa identidade africana [Por dentro da escola], que mostra formas de ensinar a história e cultura dos povos africanos. Convidando o professor de sociologia para contribuir com os assuntos referentes a sua disciplina, abordando elementos sobre indivíduo, identidade e socialização. Recurso disponível em: http://objetoseducacionais2.mec.gov.br/handle/mec/14611, acesso em 08 de novembro de 2010.
 Nossa identidade africana [Por dentro da escola]
Nossa identidade africana [Por dentro da escola]
2 - Convidar o professor de História para contribuir apresentando elementos sobre o Egito antigo, a confecção do Papiro e demais conteúdos relevantes da disciplina. Sugestão de vídeo: Do papiro à tela do computador [Livros etc.], disponível em: http://objetoseducacionais2.mec.gov.br/handle/mec/8786, acesso em 08 de novembro de 2010.
O Sistema Egípcio de Numeração. Disponível em: http://www.overmundo.com.br/banco/o-sistema-egipcio-de-numeracao, acesso em 08 de novembro de 2010.
Egipto. Disponível em: http://wwmat.mat.fc.ul.pt/~jnsilva/hm2008_9/4egipto.pdf, acesso em 08 de novembro de 2010.
Recursos Educacionais
| Nome | Tipo |
|---|---|
| Nossa identidade africana [Por dentro da escola] | Vídeo |
Recursos Complementares
A Evolução dos Numerais. Disponível em: http://www.prof2000.pt/users/hjco/numerweb/Pg000100.htm, acesso em 08 de novembro de 2010.
História do Papiro de Rhind. Disponível em: http://www.educ.fc.ul.pt/docentes/opombo/seminario/rhind/inicio.htm, acesso em 08 de novembro de 2010.
A numeração egípcia e seus símbolos. Disponível em: http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=9403, acesso em 08 de novembro de 2010.
Avaliação
A avaliação deverá ser diagnóstica, processual e continua, ou seja, realizada ao longo de todas as aulas.
Critérios a serem observados:
- Desenvolvimento e realização das atividades inicial. O aluno foi participativo? Apresentou conteúdos relevantes?
- Participação no desenvolvimento durante a explicação do professor? Foi argumentativo?
- Durante a realização das atividades? Demonstrou conhecimento?
- Na pesquisa e produção final. Participou? Produziu? Contribuiu com o grupo?
Cinco estrelas 4 classificações
- Cinco estrelas 4/4 - 100%
- Quatro estrelas 0/4 - 0%
- Três estrelas 0/4 - 0%
- Duas estrelas 0/4 - 0%
- Uma estrela 0/4 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
jaciro alves santos, Escola Municipal Cora Coralina , Goiás - disse:
jaciroalves@hotmail.com16/02/2016
Cinco estrelasParabéns, hoje ainda a professora de minha filha Stephany, passou exercícios para casa, sem no entanto, ensinar que o sistema egípcio não é posicional, o que eu considero um absurdo, visto que as crianças de outros países jamais poderiam imaginar como seria o sistema da numeração egípcia.
-
aila, condominio sapoca , Bahia - disse:
aila1luiza@gmail.com13/05/2015
Cinco estrelasEu achei bem bom até para mim que estou na escola em dia de prova <3
-
Valmir dos Santos, SESI , São Paulo - disse:
vdsants@ig.com.br08/03/2015
Cinco estrelasParabéns por essa produção. Rica em informações.
-
Cristiane Neves , Colegio Oliveira Ferreira , São Paulo - disse:
cristianeneves.2010@hotmail.com18/02/2012
Cinco estrelasAchei ótimo e vou aproveitar para dar atividades aos meus alunos.
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus