25/01/2011
Eziquiel Menta
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Educação de Jovens e Adultos - 2º ciclo | Matemática | Estatística, probabilidade e combinatória |
| Educação Escolar Indígena | Artes | Arte e pluralidade cultural |
| Ensino Médio | Matemática | Números e operações |
| Ensino Médio | Matemática | Geometria |
O que o aluno poderá aprender com esta aula
§ Identificar padrões e sequências nos sonas.
§ Realizar atividades que apresentam padrões e sequências no sonas.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Conhecimentos de cálculo e geometria.
Estratégias e recursos da aula
Professor, em sala de aula, comece essa atividade, explicando aos alunos sobre a cultura do povo Quioco.
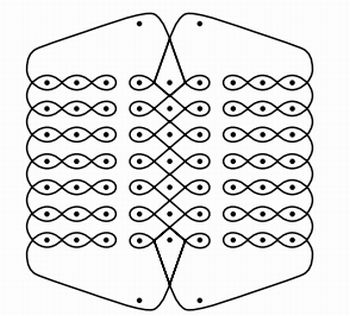
| Figura 1 - Fonte: http://www.exploratorium.edu/store_images/publications/masc_sona.pdf A população quioca vive no nordeste da Angola. É um povo de caçadores, que se dedica também a agricultura. São famosos pela sua arte. Ornamentam casas com desenhos, fabricam esteiras e cestarias decoradas. Seus desenhos são conhecidos por sona. Geralmente, executam seus desenhos na areia para ilustrar historietas, lendas e adivinhações. Reunidos no centro da aldeia, à noite em volta da fogueira ou durante o dia à sombra das árvores, os quiocos passam horas contando ou ouvindo suas histórias. Fonte: Gerdes, Paulus. Vivendo a matemática: desenhos da África. 3ª ed.,São Paulo: Scipione, 1997. 64 p. |
Vamos conhecer algumas dessas histórias...
| 1 - A cegonha e o leopardo Certo dia, o leopardo Kajama pediu à cegonha Kumbi algumas penas para forrar sua toca. Passando por um tempo, foi a ave que pediu a Kajama da sua pele. Ao atender ao pedido, o leopardo veio a morrer. Seus filhos procuraram vingar-se, mas Kumbi, que dominava bem o pântano, conseguiu escapar. No desenho, os pontinhos representam o pântano pelo qual a cegonha corria. Fonte: Gerdes, Paulus. Vivendo a matemática: desenhos da África. 3ª ed.,São Paulo: Scipione, 1997. 64 p. Figura 2 - Fonte: http://www.exploratorium.edu/store_imag es/publications/masc_sona.pdf |
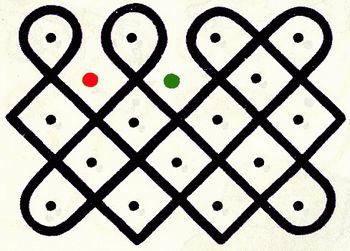
| 2 - O caçador e o cão Conta um velho narrador que certo caçador chamado Tshipinda, foi à caça levando o cão Kawa, e apanhou um cabra do mato. De volta a aldeia, o caçador dividiu a carne com Calala, o dono do cão. Kawa ficou apenas com os ossos. Depois de algum tempo, voltou Tshipinda a pedir os serviços do cão, este recusou-se a ajudá-lo. Disse ao caçador que levasse Calala, pois era com quem costumava dividir sua carne. No desenho, o ponto verde representa o caçador, e o vermelho, o caçador. Fonte: Gerdes, Paulus. Vivendo a matemática: desenhos da África. 3ª ed.,São Paulo: Scipione, 1997. 64 p. Figura 3 - Fonte: Imagem da autora |
Atividade 1
Professor, em sala de aula, proponha que os alunos (em grupos de 3 a 4 alunos) que representem um dos desenhos das duas histórias, com o cuidado de usar uma linha única e contínua. O desenho deve ser feito sem que se tire o lápis do papel. Além disso, não se pode passar uma segunda vez sobre a linha; é permitido apenas cruzá-la.
Resposta:
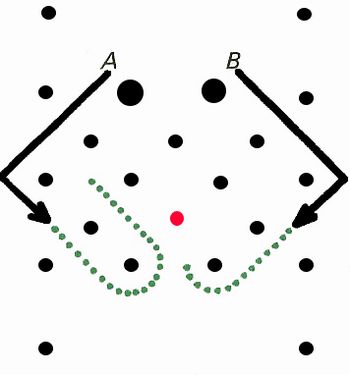
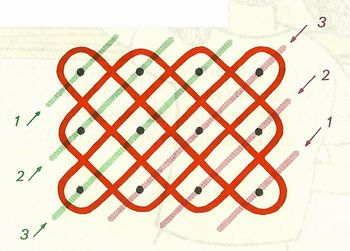
| Orientação para explicação: Para os quiocos, esses desenhos são a sua escrita. É uma liguagem composta por pontos e linhas. O narrador da história inicialmente marca os pontos na areia, fazendo uma rede retangular de pontinhos. Com filas perpendiculares às colunas. No caso dos desenhos acima, quando se começa em A, termina-se em B, e vice-versa. Fonte: Gerdes, Paulus.Vivendo a matemática: desenhos da África. 3ª ed.,São Paulo: Scipione, 1997. 64 p. A medida que os grupos estiverem realizando a atividade, peça que percebam os padrões e regularidades que compõe cada desenho. Questione se as figuras apresentam simetria. Obs. Os desenhos podem ser executados em sala de aula, com papel e lápis. Mas, se quiser, experimente que os grupos os desenhem na no chão, na terra. Figura 4 - Fonte: Imagem da autora |
Atividade 2
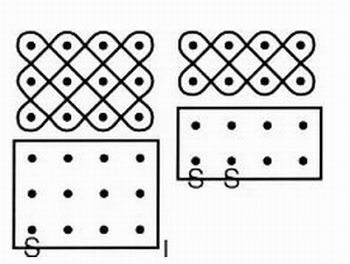
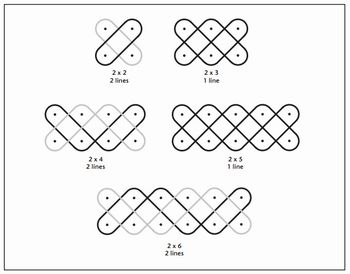
Professor, ainda nos grupos, apresente o desenho abaixo. Ele representa um dos tipos mais simples de Sona. Para desenhar a figura, solicite que os alunos pensem em uma grade retangular. No primeiro desenho temos a grade 4 X 3 e no segundo 4 X 2.
| Figura 5 - Fonte: http://academic.evergreen.edu/curricular/Patterns/Assignments/Image43.jpg Solicite que os grupos procurem realizar os dois desenhos. Na realização das atividades questione os alunos. 1- Que regularidades percebem? 2- A figura da esquerda pode ser feita com uma única curva contínua, mas o da direita exige duas curvas, porque isso ocorre? Resposta: Professor, apresentamos aqui alguns modelos de sonas desenvolvidos por meio de diferentes malhas. No material SONA - Sand Drawings from Afric (p.8 e 9), disponível em: http://www.exploratorium.edu/store_images/publications/masc_sona.pdf, acesso em 02 de dezembro de 2010, você vai encontrar outros modelos de sonas com diferentes malhas. Figura 6 - Fonte: http://www.exploratorium.edu/store_images/publications/masc_sona.pdf
Propor as atividades da aula Sona: a geometria dos desenhos traçados no chão, disponível em: http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=20876, acesso em 03 de dezembro de 2010. |
Além da questão da disposição (padrões) das malha para desenvolver os traçados, outra questão importante diz respeito a quantidade de traços necessários para se compor os desenhos quiocos.
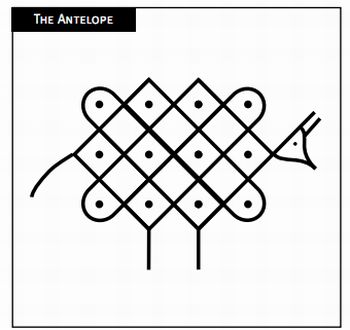
| Professor, apresente aos alunos a figura quioca (abaixo) que representa um antilope.
Figura 7 - Fonte: http://www.exploratorium.edu/store_images/publications/masc_sona.pdf Essa figura foi desenvolvida com uma malha retangular 3 x 4, ou seja, 3 filas de 4 pontinhos = 12 pontinhos. Esse desenho, nos permite contar os mesmos pontinhos de outra maneira, por meio de linhas e colunas: Figura 7 - Fonte: Gerdes, Paulus. Vivendo a matemática: desenhos da África. 3ª ed.,São Paulo: Scipione, 1997. 64 p Teremos: 1 + 2 + 3 + 3 + 2 + 1 = 2 (1 + 2 + 3) = 3 x 4 Logo: (3 x 4) Da mesma forma, se tivermos uma malha 8 colunas X 9 linhas: Teremos: 2 ( 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8) que é igual a 8 x 9 pontinhos. Se a dimensão da malha for 10 x 11, chegaremos a igualdade: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 10 x 11 2 Raciocinando da mesma maneira, podemos concluir que a soma de números de 1 a 20 é igual: ( 20 x 21) ------------- = 210 e que a soma de números naturais de 1 a 100 é igual a: (100 x 101) |
Atividade 3
Com base na explicação anterior, proponha que os alunos resolvam rapidamente as seguintes sequências, lembrando que elas remetem a uma malha "bem maior":
a) A soma do números naturais de 1 até 70.
b) A soma dos números naturais de 1 até 90.
c) A soma de números naturais de 70 até 90.
d) A soma de números naturais de 43 a 120.
Resposta:
a) (70 x 71)
-------------- = 2485
2
b) ( 90 x 91)
--------------- = 4095
2
c) 4095 - 2485 = 1610
d) (120 x 121) (42 x 43)
------------- - ----------- = 6357
2 2
1 - Propor o jogo Batalha Naval, disponível em http://objetoseducacionais2.mec.gov.br/handle/mec/9536, acesso em 12 de dezembro de 2010. Este experimento disposto na forma de jogo, permite a marcação de pontos, utilizando coordenadas cartesianas, em um tabuleiro. Os pontos marcados simbolizam embarcações de sua frota naval, onde o adversário tenta afundar as embarcações apontando as coordenadas x e y (matrizes x colunas) do ponto onde foi afixada a embarcação. O intuito dessa atividade é familiarizar os alunos com a disposição dos elementos de uma matriz em linhas e colunas.
2 - A partir da atividade desta aula e do jogo o professor pode iniciar o trabalho com matrizes e determinantes, apresentando o conteúdo da aula Desenhando com Matrizes, disponível em: http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=1915, acesso em 12 de dezembro de 2010.
Gerdes, Paulus. Vivendo a matemática: desenhos da África. 3ª ed.,São Paulo: Scipione, 1997. 64 p.
SONA - Sand Drawings from Afric, disponível em: http://www.exploratorium.edu/store_images/publications/masc_sona.pdf, acesso em 02 de dezembro de 2010.
Sona Sand Drawings. Disponível em: http://academic.evergreen.edu/curricular/Patterns/Assignments/SonaSandDrawings2.htm, acesso em 02 de dezembro de 2010.
Recursos Educacionais
| Nome | Tipo |
|---|---|
| Batalha Naval | Experimento prático |
Recursos Complementares
10 Livros, 10 Regiões, 10 Jogos para aprender e divertir-se. Disponível em: http://wwmat.mat.fc.ul.pt/~jnsilva/hm2008_9/7africa.pdf, acesso em 02 de dezembro de 2010.
GERDES, Paulus. Elementos matemáticos nos “sona”. Disponível em: http://nautilus.fis.uc.pt/bspm/revistas/20/021-027.150.pdf, acesso em 02 de dezembro de 2010.
KELLERMEIER, John. Mirror Curves. Disponível em: http://www.tacomacc.edu/home/jkellermeier/EthnomathematicsText/Chapter3/3.3MirrorCurves.htm, acesso em 02 de dezembro de 2010.
Avaliação
A avaliação deverá ser diagnóstica, processual e continua, ou seja, realizada ao longo de todas as aulas.
Critérios a serem observados:
- Desenvolvimento e participação nos momentos de explicação. Apresentou comentários relevantes? Foi argumentativo? Raciocínio adequado?
- Participação na resolução das atividades. Realizou as tarefas? Demonstrou conhecimento?
- Participação no grupo. Contribuiu com os colegas? Foi participativo?
Cinco estrelas 1 classificações
- Cinco estrelas 1/1 - 100%
- Quatro estrelas 0/1 - 0%
- Três estrelas 0/1 - 0%
- Duas estrelas 0/1 - 0%
- Uma estrela 0/1 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
lais, Instituto sagrada familia , Minas Gerais - disse:
lgf@hotmail.com02/08/2012
Cinco estrelastexto muito bom, e com ótimas informações
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus