25/01/2011
Rita Maria Cardoso Meirelles, Ivail Muniz Junior, Fernando Celso Villar Marinho, Jackson Lopes, Clayton Gonçalves Silva
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Tecnologia para a matemática |
| Ensino Médio | Matemática | Análise de dados e probabilidade |
| Educação de Jovens e Adultos - 2º ciclo | Matemática | Estatística, probabilidade e combinatória |
| Ensino Fundamental Final | Matemática | Tratamento da informação |
| Ensino Médio | Educação Física | Esporte: Valores culturais |
O que o aluno poderá aprender com esta aula
Determinar o número permutações simples de n elementos.
Determinar o número de arranjos e combinações simples de n elementos tomados p a p.
Analisar a conduta ética nos esportes.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Multiplicação de Números Naturais;
Fatorial;
Número Binomial;
Princípio Fundamental da contagem;
Árvore das possibilidades.
Estratégias e recursos da aula
Professor, para realizar essa aula, encaminhe sua turma para o laboratório de informática e solicite aos alunos que se distribuam em, no máximo, três alunos por computador.
Solicite a turma que traga giz de cera ou lápis de cor das cores verde, amarela e azul.
Nota: Para obter a folha impressa com as bandeiras acesse o link http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/Bandeiras.pdf , tire cópias e distribua.
Imagem da autora
Atividade 1:
Pintura de bandeiras retangulares com três listras
O objetivo desta atividade é construir a árvore de possibilidades e utilizá-la na elaboração do conceito de permutação simples.
Faça os questionamentos a seguir e peça aos alunos para colocarem na folha com o desenho das bandeiras o número de cada item e pintarem a quantidade necessária para satisfazer as condições dadas, utilizando apenas as cores verde, amarela e azul.
a). Quantas bandeiras de uma única cor podemos construir?
b). Quantas bandeiras com duas cores diferentes podemos pintar?
c). Quantas bandeiras com três cores diferentes podemos criar?
d). E se não houvesse bandeiras para pintar? Represente a situação da letra c utilizando a árvore de possibilidades.
e). A partir da representação feita na letra d, responda:
e.1). Quantas cores podem ser pintadas na primeira listra?
e.2). Após a pintura da primeira, quantas cores podem ser pintadas na segunda listra?
e.3). Já na terceira listra, podemos contar com quantas cores?
e.4). Como você pode relacionar estes resultados com o número de bandeiras obtidas?
Reserve um tempo para a exploração da atividade;
Após o término do tempo previsto, debata as soluções com a turma.
Nota: Todas as definições e soluções desta aula encontram-se disponíveis em http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/AnaComb.pdf . Portanto, previamente, imprima, faça cópias e distribua.
Imagem da autora
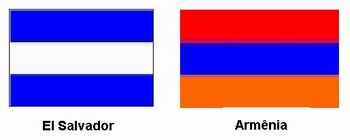
Observação: Deixe claro para todos que é também possível pintar a bandeira com apenas uma ou duas cores. Exiba com o uso do Data Show a figura abaixo como exemplos de bandeiras pintadas com apenas duas cores, para facilitar a compreensão desta observação.
Imagem editada pela autora a partir de http://www.sogeografia.com.br/Bandeiras/Africa/
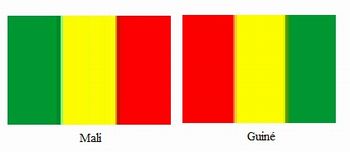
Na letra c, ressalte que a ordem na qual pintamos as listras implica bandeiras diferentes. Exiba o exemplo abaixo, no qual as bandeiras de dois países do continente africano diferem apenas pela ordem das cores. Também vale observar que há, como referência, a posição na qual a bandeira é presa ao mastro.
Imagem editada pela autora a partir de http://www.sogeografia.com.br/Bandeiras/Africa/
Na letra d, a turma deve construir a árvore de possibilidades, já na letra e os alunos devem perceber que o número de bandeiras de n listras que devem ser coloridas com n cores diferentes é dado por n!.
Conte para a turma que este exemplo trata-se de um caso de Permutação Simples.
Atividade 2:
Definição de permutação simples
Faça a construção junto com a turma no quadro de giz.
Definindo Permutação Simples: O número de permutações simples de n objetos distintos, ou seja, o número de ordens em que podemos colocar n objetos distintos é Pn = n!.
Pois, ao escolher o objeto que ocupará a primeira posição dispomos de n opções; já a escolha do segundo pode ser feita de n - 1 formas diferentes; para a terceira posição contamos com n - 2 possibilidades, etc; a escolha do objeto que ocupará o último lugar pode ser feita de 1 modo.
Portanto, temos n . (n - 1) . (n - 2) . ... . 1 = n! Lê-se: Fatorial de n ou n fatorial.
Nota: Considera-se 0!=1.
Peça aos alunos fazerem suas anotações no material recebido no início da aula que se encontra no link: http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/AnaComb.pdf
Atividade 3:
Aplicando o conceito de permutação simples em diferentes contextos
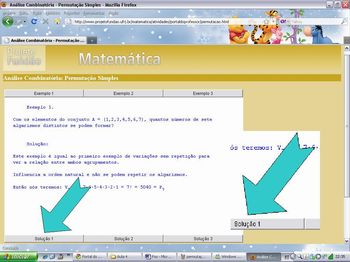
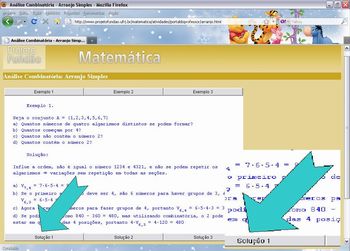
Solicite aos alunos que acessem o link http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/permutacao.html;
Exiba a página e leia junto com a turma o primeiro exemplo;
Imagem da autora
Solicite sugestões para resolvê-lo. Reserve um momento para o diálogo e troca de ideias.
Apresente e discuta a resolução do exemplo;
Nota: Para apresentar o encaminhamento da resposta, clique em solução, como está ilustrado na figura abaixo.
Imagem da autora
Repita este processo para os exemplos 2 e 3.
Atividade 4:
Campeão e vice-campeão do Campeonato Brasileiro 2010
O objetivo desta atividade é construir a árvore de possibilidades e utilizá-la na elaboração do conceito de arranjo simples.
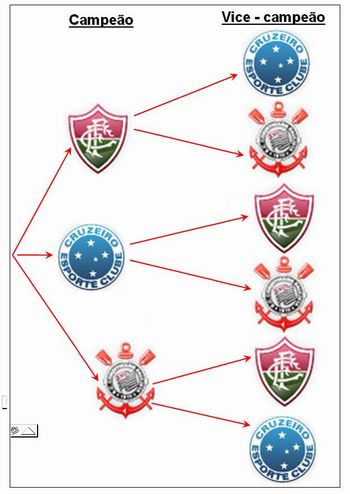
O campeonato brasileiro de 2010 foi decidido na última rodada. Pergunte a turma os nomes dos times que ficaram nesta situação. A turma deve responder Fluminense, Cruzeiro e Corinthians.
Pergunte quais seriam os possíveis resultados para campeão e vice-campeão.
Peça aos grupos que construam a árvore das possibilidades que representa este problema.
Nota: A turma deve perceber que podemos ter n times para formarem grupos de p elementos onde n é maior ou igual a p e pergunte utilizando exemplos da árvore construída se todos compreendem que neste problema a ordem também importa.
Estabeleça um tempo para a execução da atividade.
Após o tempo estabelecido, exiba a árvore de possibilidades com o auxílio do Data Show e esclareça quaisquer dúvidas dos alunos.
Imagem da autora
Conte aos alunos que este exemplo trata-se de um caso de Arranjo Simples.
Atividade 5:
Definição de arranjo simples
Faça a construção junto com a turma no quadro de giz.
Definindo Arranjo Simples:
Imagem da autora
Peça aos alunos para fazerem anotações no material que eles receberam, disponível no link: http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/AnaComb.pdf
Atividade 6:
Aplicando o conceito de arranjo simples em diferentes contextos
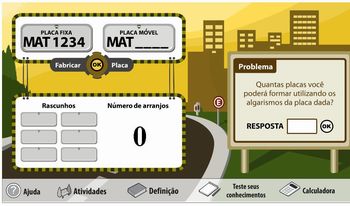
Solicite aos alunos que acessem o link http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/arranjo.html
Exiba a página e leia junto com a turma o primeiro exemplo;
Solicite sugestões para resolvê-lo. Reserve um momento para o diálogo e troca de ideias.
Apresente e discuta a resolução do exemplo;
Nota: Para apresentar o encaminhamento da resposta, clique em solução, como está ilustrado na figura abaixo.
Imagem da autora
Repita este processo para os exemplos 2 e 3.
Atividade 7:
Um aperto de mão... uma conduta ética no esporte
O objetivo desta atividade é construir a árvore de possibilidades e utilizá-la na elaboração do conceito de combinação simples.
Inicie esta atividade conversando com a turma sobre o tema transversal ética, perguntando se alguém sabe o que é uma conduta ética nos esportes.
Exemplifique citando que a gentileza do atleta, numa competição de esporte coletivo, como o futebol, ao estender a mão para auxiliar um adversário a se levantar ou o cumprimento do vencedor ao vencido, ao término de uma partida, situam-se como exemplos de ética esportiva.
Solicite um voluntário, peça ao mesmo que se levante e pergunte quantos cumprimentos ele pode fazer.
Nota: Mostre a imagem com o auxílio do Data Show para deixar claro como deve ser feito tal cumprimento.

A turma deve responder que uma pessoa não pode cumprimentar outras caso esteja sozinha em um ambiente.
Solicite outro candidato e se nenhum aluno se apresentar, escolha um aleatoriamente. Questione sobre o número cumprimentos que podem ser feitos por duas pessoas. A turma deve responder um.
Peça aos alunos para formarem grupos de quatro componentes e, através da interação, chegarem ao número de apertos de mão para três e quatro pessoas.
Após esta interação, peça aos alunos que construam a árvore de possibilidades das duas situações. Solicite a turma que utilize as letras A, B, C e D na representação dos componentes dos grupos para facilitar a correção.
Estabeleça um tempo para a execução da atividade.
Ao término do tempo estabelecido, exiba as árvores de possibilidades disponíveis em http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/AnaComb.pdf com o auxílio do Data Show e verifique com a participação de todos as respostas dadas pelos grupos.
Atividade 8:
Definição de combinação simples
Faça a construção junto com a turma no quadro de giz.
Definindo Combinação Simples:
Imagem da autora
Peça aos alunos para fazerem anotações no material que eles receberam, disponível no link: http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/AnaComb.pdf .
Atividade 9:
Aplicando o conceito de combinação simples em diferentes contextos
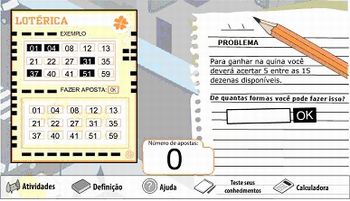
Solicite aos alunos que acessem o link http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/combinacoes.html
Exiba a página e leia junto com a turma o primeiro exemplo;
Solicite sugestões para resolvê-lo. Reserve um momento para o diálogo e troca de ideias.
Apresente e discuta a resolução do exemplo;
Nota: Para apresentar o encaminhamento da resposta, clique em solução, como está ilustrado na figura abaixo.
Imagem da autora
Repita este processo para os exemplos 2 e 3.
Atividade 10:
Explorando os conceitos construídos
Para solidificar os conceitos construídos solicite a turma que acesse os links a seguir e iniciem as atividades.
Determine um tempo para o desenvolvimento da atividade e em seguida, circule pelo laboratório para observar o desenvolvimento dos alunos.
Valorize o desenvolvimento do raciocínio em detrimento da aplicação de fórmulas.
- Explorando as permutações simples: http://rived.mec.gov.br/atividades/matematica/permutacao/permutacao.swf
Imagem editada pela autora a partir de
http://rived.mec.gov.br/atividades/matematica/permutacao/permutacao.swf
- Explorando os arranjos simples: http://rived.mec.gov.br/atividades/matematica/arranjo/arranjo.swf
Imagem editada pela autora a partir de
http://rived.mec.gov.br/atividades/matematica/arranjo/arranjo.swf
- Explorando as combinações simples: http://rived.mec.gov.br/atividades/matematica/combinacao/combinacao.swf
Imagem editada pela autora a partir de
http://rived.mec.gov.br/atividades/matematica/combinacao/combinacao.swf
A turma pode utilizar o recurso educacional abaixo para conferir os resultados encontrados.
Primeiro Momento
O artigo Número de regiões: um problemade contagem mostra a análise de um problema de contagem do número de regiões no plano que pode ser resolvido de maneira direta, simples e interessante. Acesse o material do Portal do Professor disponível em http://portal.mec.gov.br/seb/arquivos/pdf/EnsMed/expensmat_3_4e5.pdf e faça as adaptações para se adequarem à realidade da sua sala de aula.
Obs. Este é o quarto artigo deste arquivo.
Imagem editada pela autora a partir de
http://portal.mec.gov.br/seb/arquivos/pdf/EnsMed/expensmat_3_4e5.pdf
Segundo Momento
Retome o tema transversal ética e mostre algumas reportagens disponíveis em:
http://www.cidadedofutebol.com.br/Jornal/Colunas/Detalhe.aspx?id=10784
http://www.futsalbrasil.com.br/artigos/artigo.php?cd_artigo=148
Exiba com o uso do Data show a reportagem O dopping no esporte, exibida em 29/09/2009, integrante de uma série de reportagens que tratam do tema Rio e as Olimpíadas de 2016, para a turma ver um exemplo de conduta anti-ética, obter informações sobre o dopping e tomar conhecimento que o Brasil possui um dos mais modernos laboratórios antidopping do mundo.
Para tanto acesse o link: http://www.youtube.com/watch?v=Q5SSnb6lKrs&feature=related
Imagem editada pela autora a partir de http://www.youtube.com/watch?v=Q5SSnb6lKrs&feature=related
Peça a turma que pesquise na internet sobre o tema Conduta ética e anti-ética na prática desportiva.
Após a pesquisa, a leitura das reportagens e a apresentação do vídeo realize um debate sobre os temas ética nos esportes e em sala de aula.
Recursos Educacionais
| Nome | Tipo |
|---|---|
| Combinatória | Software Educacional |
Recursos Complementares
Fontes de pesquisa:
1. Aulas que complementam o assunto:
A Matemática nos Esportes: Analisando Dados em Gráficos Setoriais - http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=22698
2. Sobre o tema transversal ética:
http://portal.mec.gov.br/seb/arquivos/pdf/livro082.pdf
http://www.apagina.pt/?aba=7&cat=167&doc=12358&mid=2
http://www.revistadeeducacaofisica.com.br/artigos/2004/condutaseticas.pdf
3. Sobre as definições:
As definições foram adaptadas do livro Matemática, volume único: livro do professor/ Luiz Roberto Dante. 1 ed. – São Paulo: Ática – 2005.
Link: http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/Livro.pdf
4. Software Nippe Descartes
O grupo de pesquisa “Tecnologias no Ensino da Matemática”, vinculado ao Projeto Fundão, confeccionou diversas atividades utilizando o software Nippe Descartes, um aplicativo desenvolvido em Java que permite uma manipulação ágil e simples de janelas gráficas aplicáveis a qualquer página web. Este grupo reúne-se semanalmente e se propõe a desenvolver aplicações específicas para apresentação de conteúdos do Ensino Médio.
Página do Projeto Fundão: http://www.projetofundao.ufrj.br/matematica/
Para visualizar as atividades o professor deve:
a). Baixar o software Java disponível em: http://www.java.com/pt_BR/download/
b). Baixar o arquivo contendo as atividades.
Avaliação
Aplicação de problemas visando a avaliação do conteúdo apresentado.
O link abaixo apresenta sugestões de exercícios para serem aplicados ao final desta aula.
http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/AnaCombAluno.pdf
As soluções dos problemas propostos se encontram no link abaixo:
http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/AnaCombProfessor.pdf
Cinco estrelas 1 classificações
- Cinco estrelas 1/1 - 100%
- Quatro estrelas 0/1 - 0%
- Três estrelas 0/1 - 0%
- Duas estrelas 0/1 - 0%
- Uma estrela 0/1 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
juscimeire da silva caldeira, EEMARIA MACEDO RODRIGUES , Mato Grosso - disse:
juscicaldeira@hotmail.com01/02/2011
Cinco estrelasmuito boa
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus