13/01/2011
Rita Maria Cardoso Meirelles, Ivail Muniz Junior; Fernando Celso Villar Marinho, Jackson Lopes, Clayton Gonçalves Silva, Raquel Cupolillo Simões de Sousa
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Educação Profissional | Gestão e Negócios | Técnico em Operações Administrativas |
| Ensino Médio | Matemática | Números e operações |
| Educação Profissional | Gestão e Negócios | Técnico em Operações Financeiras |
| Educação Profissional | Gestão e Negócios | Técnico em Transações Imobiliárias |
| Ensino Médio | Matemática | Álgebra |
| Educação Profissional | Gestão e Negócios | Técnico em Contabilidade |
| Educação Profissional | Gestão e Negócios | Técnico em Vendas |
| Educação Profissional | Gestão e Negócios | Técnico em Cooperativismo |
| Educação Profissional | Gestão e Negócios | Técnico em Operações Comerciais |
O que o aluno poderá aprender com esta aula
- Sistemas de amortização de empréstimos;
- O Sistema de Amortizações Constantes (SAC) com e sem carência;
- Calcular o saldo devedor, os juros e o valor das prestações após o pagamento de uma prestação qualquer;
- Criar e entender a tabela SAC.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
- Porcentagem;
- Fator de atualização — um capital C, aumentado de uma taxa i, fica multiplicado por (1 + i).
- Progressão Geométrica.
- Visite: "Juros Compostos e P.G." ( http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=24132).
Estratégias e recursos da aula
Os sistemas de amortização são formas de pagamentos de um financiamento. Há diferentes tipos de sistemas de amortização. Aprenderemos nessas atividades o Sistema de Amortização Constante.
Primeiro é preciso entender o que é Amortizar.
Amortizar é pagar aos poucos uma dívida.
Segundo é preciso entender que quando se paga uma prestação, parte do valor pago quita a dívida e parte paga os juros. Por exemplo: Se o saldo devedor em um mês é 100 reais e a taxa é de 10% ao mês, após 1 mês, uma prestação de 18 reais reduz a dívida em 8 reais, pois 10 reais serão gastos para pagar os juros desse mês.
As atividades abaixo mostrarão como funciona o Sistema de Amortização constante, o qual, como o próprio nome já sugere, amortiza a dívida sempre de um mesmo valor. Ele é muito utilizado em financiamento de imóveis, sendo menos utilizado em financiamento de bens de consumo.
Vamos à aula.
ATIVIDADE 1.
Nessa atividade construiremos um sistema de amortização não definido, apenas para ajudar o aluno a compreender o funcionamento de uma tabela de amortização. O objetivo aqui, portanto, não será ainda estudar o SAC, mas conhecer os fundamentos presentes em qualquer sistema de amortização.
1) Inicialmente, peça que cada aluno, individualmente preencha a tabela abaixo, a partir das informações da situação apresentada.
Valor Financiado = R$ 300,00
Taxa = 10% ao mês
| Mês |
Prestação |
Juros |
Amortização |
Saldo devedor |
| 0 |
|
|
|
300,00 |
| 1 |
|
|
90,00 |
|
| 2 |
|
|
90,00 |
|
| 3 |
|
|
120,00 |
|
Imagem do autor.
2) Amortizar significa pagar parte da dívida aos poucos, ou ainda, extinguir (a dívida) aos poucos. Assim, explique porque uma pessoa paga a primeira prestação no valor de R$ 120,00, mas o saldo se reduz apenas de R$90,00?.
3) A amortização da dívida dar-se-á de forma constante ao longo dos meses?
4) Os juros decresceram? E as prestações? Explique porque isso aconteceu.
5) Refaça a tabela acima para essa nova situação, considerando agora valores de amortização mensais iguais.
| Mês |
Prestação |
Juros |
Amortização |
Saldo devedor |
| 0 |
|
|
|
300,00 |
| 1 |
|
|
100,00 |
|
| 2 |
|
|
100,00 |
|
| 3 |
|
|
|
|
Imagem do autor.
6) Qual o comportamento das prestações ao longo do tempo?
7) Qual o comportamento dos juros mensais pagos ao longo do tempo?
8) Qual o comportamento do saldo devedor ao longo do tempo?
9) Explique a relação entre os três comportamentos anteriormente observados.
10) Termine a atividade exibindo um pequeno vídeo, sobre sistemas de amortização, disponível no link indicado abaixo da imagem.
| Periodo |
Prestação |
Juros |
Amortização |
Saldo devedor |
| 0 |
|
|
|
300,00 |
| 1 |
120,00 |
30,00 |
90,00 |
210,00 |
| 2 |
111,00 |
21,00 |
90,00 |
120,00 |
| 3 |
132,00 |
12,00 |
120,00 |
0,00 |
Imagem do autor.
| Periodo |
Prestação |
Juros |
Amortização |
Saldo devedor |
| 0 |
|
|
|
300,00 |
| 1 |
130,00 |
30,00 |
100,00 |
200,00 |
| 2 |
120,00 |
20,00 |
100,00 |
100,00 |
| 3 |
110,00 |
10,00 |
100,00 |
0,00 |
Imagem do autor.
ATIVIDADE 2
Nessa atividade construiremos mais uma vez um sistema de amortização constante - SAC com o objetivo de fixar a estrutura e composição das amortizações e prestações desse sistema.
1) Divida a turma em grupos de quatro pessoas e apresente o caso de SAC, conforme abaixo.
O Caso de Silvio Antonio Costa
Silvio quer comprar um carro e decidiu comprar pelo SAC. O valor do carro é de R$ 40.000,00 e ele dará de entrada o valor de seu carro, estimado em R$ 16.000,00 pela própria agência que venderá o carro novo. Ele optou por um parcelamento em apenas 12 prestações, para usufruir de uma taxa de juros menor, igual a 0,8% ao mês, e além disso não pagar TAC nem outras despesas adicionais.
Preencha a tabela de amortização para esse sistema.
| Mês |
Prestação |
Juros |
Amortização |
Saldo devedor |
| 0 |
|
|
|
|
| 1 |
|
|
|
|
| 2 |
|
|
|
|
| 3 |
|
|
|
|
| 4 |
|
|
|
|
| 5 |
|
|
|
|
| 6 |
|
|
|
|
| 7 |
|
|
|
|
| 8 |
|
|
|
|
| 9 |
|
|
|
|
| 10 |
|
|
|
|
| 11 |
|
|
|
|
| 12 |
|
|
|
|
Imagem do autor.
Analisando o sistema de financiamento.
a) Qual o primeiro passo para se montar a tabela de amortização no sistema SAC.
b) As prestações decrescem em Progressão Aritmética? Por que? Qual a razão?
c) Qual o comportamento das prestações ao longo do tempo?
d) Qual o comportamento dos juros mensais pagos ao longo do tempo?
e) Qual o comportamento do saldo devedor ao longo do tempo?
f) Explique a relação entre os três comportamentos anteriormente observados.
g) Se ele não desse o carro de entrada, em quantos reais a mais primeira prestação subiria? E as outras?
h) Quais as vantagens e desvantagens do sistema SAC?
| Periodo |
Prestação |
Juros |
Amortização |
Saldo devedor |
| 0 |
|
|
|
24000,00 |
| 1 |
2192,00 |
192,00 |
2000,00 |
22000,00 |
| 2 |
2176,00 |
176,00 |
2000,00 |
20000,00 |
| 3 |
2160,00 |
160,00 |
2000,00 |
18000,00 |
| 4 |
2144,00 |
144,00 |
2000,00 |
16000,00 |
| 5 |
2128,00 |
128,00 |
2000,00 |
14000,00 |
| 6 |
2112,00 |
112,00 |
2000,00 |
12000,00 |
| 7 |
2096,00 |
96,00 |
2000,00 |
10000,00 |
| 8 |
2080,00 |
80,00 |
2000,00 |
8000,00 |
| 9 |
2064,00 |
64,00 |
2000,00 |
6000,00 |
| 10 |
2048,00 |
48,00 |
2000,00 |
4000,00 |
| 11 |
2032,00 |
32,00 |
2000,00 |
2000,00 |
| 12 |
2016,00 |
16,00 |
2000,00 |
0,00 |
Imagem do autor.
ATIVIDADE 3
Nessa atividade construiremos um sistema de amortização constante – SAC, como ponto de partida para construir um outro sistema de amortização, chamado SAM – Sistema de Amortização mista, com o objetivo de fixar a estrutura e composição das amortizações e prestações desse sistema. Além disso, proporemos aos alunos a criação de um sistema de amortização segundo critérios próprios.
1) Divida a turma em grupos de quatro pessoas e apresente duas tabelas de amortização de um financiamento de R$ 1.000,00, a uma taxa de 10% ao período, financiado em 5 prestações mensais.
| Sistema de Amortização Constante |
| Periodo |
Prestação |
Juros |
Amortização |
Saldo devedor |
| 0 |
|
|
|
1.000,00 |
| 1 |
300,00 |
100,00 |
200,00 |
800,00 |
| 2 |
280,00 |
80,00 |
200,00 |
600,00 |
| 3 |
260,00 |
60,00 |
200,00 |
400,00 |
| 4 |
240,00 |
40,00 |
200,00 |
200,00 |
| 5 |
220,00 |
20,00 |
200,00 |
0,00 |
Imagem do autor.
| Sistema de Amortização Francês |
| Periodo |
Prestação |
Juros |
Amortização |
Saldo devedor |
| 0 |
|
|
|
1000,00 |
| 1 |
263,80 |
100,00 |
163,80 |
836,20 |
| 2 |
263,80 |
83,62 |
180,18 |
656,03 |
| 3 |
263,80 |
65,60 |
198,19 |
457,83 |
| 4 |
263,80 |
45,78 |
218,01 |
239,82 |
| 5 |
263,80 |
23,98 |
239,82 |
0,00 |
Imagem do autor.
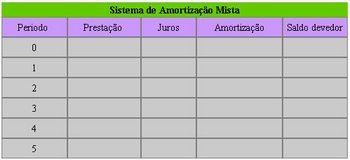
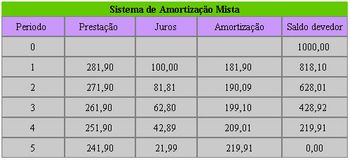
2) Proponha aos grupos que criem um sistema de amortização mista em que cada prestação é a média aritmética da prestação do SAC com a do sistema Francês. Peça para preencherem um nova tabela com esse sistema.
Imagem do autor.
3) Peça aos grupos para produzirem um relatório explicando a composição desse novo sistema. Nessa análise, os alunos podem utilizar os roteiros anteriores como referência e perguntas a serem respondidas.
4) Por último, peça aos grupos para criarem seu próprio sistema de financiamento e a planilha de amortização referida. Estabeleça um valor inicial, uma taxa e um número de prestações, de 4 a 12 para não entediar os alunos com a repetição das operações. Uma sugestão é utilizar uma planilha eletrônica para a tarefa.
Imagem do autor.
Recursos Complementares
Aula do Portal do Professor
Matemática Financeira: O valor do dinheiro no tempo
(http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=25767)
Vídeos
Consumo e orçamento das famílias.
http://www.youtube.com/watch?v=51mbDDhq9gQ
Planejamento Financeiro.
http://www.youtube.com/watch?v=rp39kUJSuZg
Uma aula especial de Matemática Financeira do Professor Augusto C. de O. Morgado, está disponível em http://video.impa.br/index.php?page=janeiro-de-2007. NÃO DEIXE DE ASSISTIR!!!
Avaliação
- Avaliação individual. Aplicar problemas e situações em que o aluno mostre como utilizar os conceitos apresentados para atacar e resolver situações financeiras.
- Avaliação coletiva. Resolução de problemas que requeiram pesquisa de informações na Internet, como por exemplo, em que situações os bancos financiam pelo SAC e por outros sistemas; quais as taxas praticadas no mercado.
Sem estrelas 0 classificações
- Cinco estrelas 0/0 - 0%
- Quatro estrelas 0/0 - 0%
- Três estrelas 0/0 - 0%
- Duas estrelas 0/0 - 0%
- Uma estrela 0/0 - 0%
Denuncie opiniões ou materiais indevidos!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus