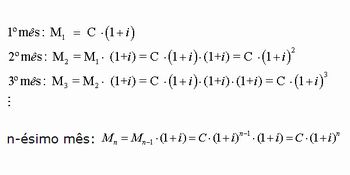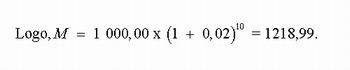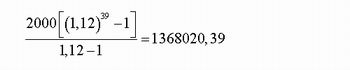04/11/2010
Fernando Celso Villar Marinho, Rita Maria Cardoso Meirelles
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Álgebra |
| Ensino Médio | Matemática | Análise de dados e probabilidade |
| Educação Profissional | Gestão e Negócios | Técnico em Contabilidade |
| Educação Profissional | Gestão e Negócios | Técnico em Vendas |
| Educação de Jovens e Adultos - 2º ciclo | Matemática | Grandezas e medidas |
| Educação Profissional | Gestão e Negócios | Técnico em Operações Financeiras |
| Ensino Médio | Matemática | Números e operações |
| Educação Profissional | Gestão e Negócios | Técnico em Operações Administrativas |
| Educação Profissional | Gestão e Negócios | Técnico em Operações Comerciais |
O que o aluno poderá aprender com esta aula
Relacionar juros compostos com sequências numéricas;
Interpretar Progressões Geométricas buncando a construir o conceito de Juros Compostos;
Calcular Juros Compostos.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Frações e Porcentagem.
Notação decimal.
Juros simples.
Progressão geométrica.
Reconhecimento de taxas.
Períodos de aplicação.
Estratégias e recursos da aula
O objetivo desta aula é mostrar ao aluno que os juros compostos estão ligeiramente ligados as progressões geométricas, e que este reconhecimento é bastante útil para algumas análises posteriores.
Atividade 1
Peça para os alunos pesquisarem na Internet o que é ANATOCISMO e JUROS COMPOSTOS. Por exemplo, um link com informações detalhadas é dado a seguir
Os alunos podem utilizar sites de busca como, por exemplo, Google (http://www.google.com.br)
Após essa etapa, convide os alunos a explicarem os conceitos de ANATOCISMO e JUROS COMPOSTOS. Promova um debate sobre o tema “juros sobre juros”. Esse tema será aprofundado na atividade 3.
Anatocismo é o termo jurídico utilizado para designar a capitalização de juros, isto é, a cobrança de juros sobre juros.
É importante que os alunos observem como a legislação brasileira trata o ANATOCISMO. Se for possível, convide um advogado para aprofundar este tema. Este aspecto é importante para a formação de cidadãos críticos.
Atividade 2
1º) Apresente aos alunos as definições a seguir e construa a tabela com eles, no quadro-negro.
DEFINIÇÕES BÁSICAS
REGIME DE CAPITALIZAÇÃO
É a forma assumida pelo crescimento do capital. O regime pode ser de capitalização simples ou composta. No regime de capitalização simples o juro incide exclusivamente sobre o capital inicial. O montante, neste caso, resulta de um processo de crescimento linear do capital. No regime de capitalização composta, o juro incide sobre o capital inicial bem como sobre os juros acumulados, obtendo-se um montante que resulta de um crescimento exponencial do capital. A Tabela abaixo mostra a diferença de valores finais obtidos para uma mesmo capital de R$ 5.000,00 aplicado a uma taxa de juros de 4,5 % a. m. ao final dos períodos indicados nos casos de regime de capitalização simples e composta.
JUROS COMPOSTOS
No Regime de Capitalização Composta a forma de cálculo dos juros é conhecida como juros compostos, também chamados de juros sobre juros. Enquanto o cálculo a juros simples é conhecido como cálculo linear, o cálculo a juros compostos é conhecido por cálculo exponencial de juros. Neste regime de capitalização os juros de um período são incorporados ao capital para o período subsequente.
TABELA II - Comparação de regimes de capitalização
| CAPITALIZAÇÃO SIMPLES VERSUS COMPOSTA |
| VALOR DA APLICAÇÃO |
TAXA DE JUROS (% a. m.) |
PRAZO DE APLICAÇÃO (em meses) |
MONTANTE PELO REGIME DE CAPITALIZAÇÃO SIMPLES |
MONTANTE PELO REGIME DE CAPITALIZAÇÃO COMPOSTA |
| R$ 5.000,00 |
4,50% |
1 |
R$ 5.225,00 |
R$ 5.225,00 |
| R$ 5.000,00 |
4,50% |
2 |
R$ 5.450,00 |
R$ 5.460,13 |
| R$ 5.000,00 |
4,50% |
3 |
R$ 5.675,00 |
R$ 5.705,83 |
| R$ 5.000,00 |
4,50% |
4 |
R$ 5.900,00 |
R$ 5.962,59 |
| R$ 5.000,00 |
4,50% |
5 |
R$ 6.125,00 |
R$ 6.230,91 |
| R$ 5.000,00 |
4,50% |
6 |
R$ 6.350,00 |
R$ 6.511,30 |
2º) Agora é a vez dos alunos. Peça para eles resolverem o seguinte problema: Calcular o montante de uma aplicação de R$ 1 000,00 à taxa de 10% ao mês, no regime de capitalização composto, durante 4 meses.
3º) Dê destaque ao comentário a seguir.
Os valores obtidos a cada período formam uma Progressão Geométrica, cujo primeiro termo é e a razão é (1+i).
4º) Após corrigir o problema anterior, deixe-o no quadro negro e peça para os alunos tentarem resolver esta situação generalizada. Nosso objetivo é relacionar juros compostos com PG. Enuncie a versão generalizada do problema anterior:
Calcular o montante obtido a partir de um capital C aplicado a uma taxa percentual i, no regime de capitalização composto por um período n (meses).
Atividade 3
Um banco empresta R$ 1 000,00 a juros de 2% ao mês pelo prazo de 10 meses com capitalização composta. Qual o montante a ser recebido após decorrido o período?
É importante ressaltar que a taxa (i) e o período (n) devem estar na mesma unidade de tempo.
C = 1 000,00; n = 10 meses; i = 2% a.m.
Atividade 4
Disponibilize para os alunos o texto original da reportagem 13º Salário, exibida no Jornal Hoje, em 26/06/2007.
Há uma versão disponível para impressão no link abaixo:
Décimo terceiro salário
Reportagem do Jornal Hoje, Edição do dia 26/06/2007.
Você está interessado em obter empréstimo no valor do seu décimo terceiro? O Jornal Hoje fez as contas e mostra agora para quem isso vale à pena.
Estamos no meio do ano e os bancos não se cansam de oferecer empréstimos tendo como garantia o 13° salário dos clientes. A operação aparentemente é simples e baseada no valor que o trabalhador tem direito a receber no fim do ano. Os especialistas fazem questão de lembrar que este é um empréstimo como outro qualquer. A diferença é que ele oferece menos risco para o banco, que sabe que o cliente vai ter dinheiro em dezembro. Os consultores dizem que é importante duas contas: uma que o banco faz, outra que você deve fazer.
O professor José Dutra Sobrinho simulou uma operação desse tipo. Tomamos como base um contrato feito hoje e que será pago com o 13º, a ser recebido em 20 de dezembro. O valor é de R$1.000, com prazo de 178 dias. A taxa de juros cobrada pelo banco, no nosso exemplo, é de 3% ao mês. Além dela serão cobrados 4% de taxa de abertura de crédito (R$40,00) e IOF (R$7,60). O total fica em R$1.047,60.
Os bancos fazem o cálculo com base no chamado juro composto. É assim: os juros são aplicados sobre o valor da divida acumulada. Isso acontece no primeiro mês (R$1.079,03), no segundo (R$1.111,40), no terceiro (R$1.144,74), no quarto (R$1.179,08), no quinto (R$1.214,46) e no sexto mês, quando o valor da divida chegou a R$1.248,43. Isso significa dizer que a taxa de juros efetiva no final foi de 3,8%.
E mais: se você estiver com saldo negativo, a cobrança é feita de todo jeito. E aí você passa a pagar juros de mercado sobre o saldo devedor. “Esse tipo de empréstimo é vantajoso para aquelas pessoas que podem estar endividadas numa outra modalidade, por exemplo, cheque especial e cartão de crédito, que são os grandes vilões de nosso mercado em matéria de taxa. A taxa do cheque especial deve oscilar em torno de 8% a 10%. No caso do cartão de crédito, cujas taxas oscilam de 10% a 13% ao mês, não precisa nem falar”, diz o matemático.
Fonte: http://g1.globo.com/jornalhoje/0,,MUL1156191-16022,00-DECIMO+TERCEIRO+SALARIO.html
Para pensar: Por que “esse tipo de empréstimo é vantajoso para aquelas pessoas que podem estar endividadas numa outra modalidade, por exemplo, cheque especial e cartão de crédito”?
Peça para os alunos responderem o “para pensar”. Em seguida peça a eles para explicarem as contas apresentadas no texto.
Atividade 5
Exiba para a turma o vídeo a seguir para ilustrar uma possibilidade de socialização dos conceitos de matemática financeira. Os alunos do Ensino Médio deverão elaborar atividades similares às apresentadas no vídeo para os alunos de séries iniciais. É importante estimular a integração dos alunos. O exemplo visto na reportagem mostra que esta atividade é possível e válida.
Note que nesta atividade todos tem um papel: gerente, caixa, fiscal, etc. Além disso, quem trabalha recebe um “salário” e gasta como quiser, geralmente na loja de doces, também é administrada pelos alunos.
Professor, estimule a criatividade dos alunos e a integração com os alunos mais jovens. Neste caso é fundamental a parceria com professores das séries anteriores. Se possível estabeleça um trabalho envolvendo outras disciplinas como geografia, por exemplo, ao tratar de temas como impostos.
Atividade 6
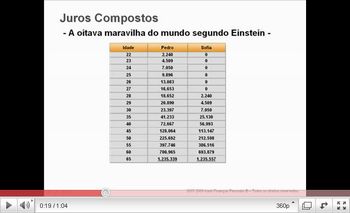
Os conceitos de soma dos termos de uma progressão geométrica são fundamentais para resolução de problemas de matemática financeira. Exiba o vídeo a seguir e peça para os alunos tentarem explicar qual a mensagem principal do texto, justificando a resposta.
Obs: a taxa anual de juros utilizada nos cálculos do vídeo é de 12% e não 11% como mostrado nas imagens. Além disso, por conta de algumas aproximações os valores podem não parecer todos corretos. O importante deste vídeo é a mensagem apresentada e a vantagem em começar a poupar o mais cedo possível.
http://www.youtube.com/watch?v=J1-dVgnWbZs
Vamos resolver um problema análogo, neste caso vamos mudar para nossa realidade.
a) Qual será o montante acumulado por Rita quando ela completar 65 anos, sabendo que ela guarda 2000 reais por ano, nos seis primeiros anos, num investimento com rendimento de 12% ao ano começando aos 21 anos de idade e depois não faz nenhum outro depósito ou retirada, deixando o dinheiro render?
b) Qual o montante acumulado por Fernando, sabendo que ele guarda 2000 reais por ano, num investimento com rendimento de 12% ao ano começando aos 27 anos de idade e terminando com 65?
a) Rita faz 6 depósitos, o primeiro aos 21 anos e o último aos 27 anos. O primeiro depósito irá render por 65-21= 45 anos.
O 1º depósito renderá ao final do período: 2000x(1,12)45= 327975,21
De forma análoga podemos calcular o valor relativo ao acumulado correspondente a cada um dos 6 depósitos.
| Depósito |
Cálculo |
Valor (em reais) |
| 1º |
2000x(1,12)44 |
292835,01 |
| 2º |
2000x(1,12)43 |
261459,83 |
| 3º |
2000x(1,12)42 |
233446,27 |
| 4º |
2000x(1,12)41 |
208434,17 |
| 5º |
2000x(1,12)40 |
186101,94 |
| 6º |
2000x(1,12)39 |
166162,45 |
Como os seis depósitos tiveram os rendimentos acumulados, para obter o valor total que a Rita terá ao final do período devemos somar os valores da última coluna, obtendo assim, R$1348439,68.
b) No caso do Fernando, o raciocínio é análogo, mas é interessante utilizar outra estratégia de cálculo. O primeiro depósito dele irá render por 65-27=38 anos e o penúltimo depósito irá render por 1 ano e o último não irá ter tempo para render.Somando os valores dos rendimentos de todos os depósitos obtemos
2000x(1,12)38+2000x(1,12)37+...+2000x(1,12)1+2000x(1,12)0
A expressão acima corresponde a soma dos 39 termos de uma PG de razão (1,12) e primeiro termo igual a 2000x(1,12)0=2000
Portanto essa soma é igual a
Note que Fernando investiu R$2000,00 reais, durante 38 anos e, mesmo assim, tem praticamente o mesmo do que Rita que investiu R$2000,00 reais, durante apenas 6 anos!
Esse exemplo ilustra bem a relação importante existente entre a progressão geométrica e os juros compostos.
Atividade 7
Depois de trabalhados os conceitos e os exemplos de atividades acima, proponha os seguintes problemas aos alunos:
- Um banco paga o montante de R$ 3 000,00 a quem aplicar em um de seus títulos durante 5 meses. Sabendo que a taxa de juros é de 2% ao mês, qual o valor do capital necessário neste investimento?
- Um capital de R$ 1 500,00 foi aplicado a taxa de 10% ao ano e obteve um montante de R$ 2 390,61. Quanto tempo esse capital ficou aplicado?
- Calcular o montante de uma aplicação de R$ 10 000,00 considerando a taxa de juros de 5% ao semestre por um tempo de 3 anos e meio.
http://www.projetofundao.ufrj.br/matematica/images/stories/matfin.jpg
Professor, estimule o uso de calculadoras em todas as atividades!
1. Montante: R$ 3 000,00
n = 5 meses
Portanto temos M = 3 000,00; n = 5; i = 2% a.m.
Logo, 3 000,00 = C x (1 + 0,02)5
C = 3 000,00 / (1 + 0,02)5 = 2 717,40
2. Capital aplicado: R$ 1 500,00
Montante obtido: R$ 2 390,61
Portanto temos C = 1 500,00; M = 2 390,61; i = 10% a.a.
Logo, 2 390,61 = 1 500,00 x (1 + 0,1)n
(1,1)n = 2 390,61 / 1 500,00
(1,1)n = 1,594
log (1,1)n = log (1,594)
n log (1,1) = log (1,594)
n = log (1,594)/ log (1,1)= 4,89
Portanto, n é aproximadamente 5.
3.Aplicação: R$ 10 000,00
n = 3 anos e meio; n = 7 semestres, pois um semestre corresponde a 6 meses
Portando temos C = 10 000,00; n = 7; i = 5% a.s.
Logo, M = 10 000,00 x (1 + 0,05)7 = 14 071,00
Recursos Complementares
Acesso aos links:
http://www.projetofundao.ufrj.br/matematica/index.php?option=com_content&task=view&id=6&Itemid=18
Aulas do Portal
• Matemática Financeira no CAp UFRJ: Introdução
http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=9918
• Matemática Financeira no CAp UFRJ: Juros Compostos
http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=9932
• Matemática Financeira no CAp UFRJ: Equivalência de Capitais
http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=9935
• Matemática Financeira no CAp UFRJ: Equivalência de Taxas
http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=9939
• Matemática Financeira no CAp UFRJ: Cálculo de Prestações
http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=10063
• Matemática Financeira no CAp UFRJ: Cálculo de Taxa de Juros
http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=10069
• Matemática Financeira no CAp UFRJ: Opções de Pagamento
http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=12978
• Matemática Financeira no CAp UFRJ: Opções de Pagamento e o Excel
http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=13004
• Matemática Financeira no CAp UFRJ: Sistemas de Amortização
http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=12982
• Matemática Financeira no CAp UFRJ: Tabela Price e o Planilhas Eletrônicas
http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=12989
• Matemática Financeira no CAp UFRJ: SAC e o Planilhas Eletrônicas
http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=12991
Avaliação
A avaliação deve ser feita ao longo de toda a aula baseada na participação dos alunos nas atividades propostas.
Outra possibilidade é propor que os alunos resolvam, em grupos, as atividades presentes na aula "Matemática Financeira no CAp UFRJ: Juros Compostos" (http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=9932).
Valorize o raciocínio e não as fórmulas!
Cinco estrelas 2 classificações
- Cinco estrelas 2/2 - 100%
- Quatro estrelas 0/2 - 0%
- Três estrelas 0/2 - 0%
- Duas estrelas 0/2 - 0%
- Uma estrela 0/2 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
felipe nazário da silva, EEB ABILIO CESAR BORGES , Santa Catarina - disse:
felippenazario@hotmai.com09/08/2013
Cinco estrelasmuito bem aplicado. pode-se trabalhar o conceito matemático de PG juntamente com a capitalização de juros compostos.
-
Luzia, CE ESTADO DE SÃO PAULO , Maranhão - disse:
luinzr@gmail.com20/01/2011
Cinco estrelasGostei muito desta aula, pois trabalhei o assunto na 8ª série (9º ano).
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus