13/12/2010
Rita Maria Cardoso Meirelles, Ivail Muniz Junior, Fernando Celso Villar Marinho, Jackson Lopes, Clayton Gonçalves Silva, Raquel Cupolillo Simões de Sousa.
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Educação Profissional | Gestão e Negócios | Técnico em Transações Imobiliárias |
| Educação Profissional | Gestão e Negócios | Técnico em Operações Comerciais |
| Ensino Médio | Matemática | Números e operações |
| Educação Profissional | Gestão e Negócios | Técnico em Operações Financeiras |
| Educação Profissional | Gestão e Negócios | Técnico em Contabilidade |
| Educação de Jovens e Adultos - 2º ciclo | Matemática | Proporcionalidade e Equivalência |
| Educação Profissional | Gestão e Negócios | Técnico em Vendas |
O que o aluno poderá aprender com esta aula
a diferença entre taxa nominal e efetiva.
que uma taxa está sempre referida a um período. Taxa e tempo são inseparáveis.
que em algumas situações, há um péssimo hábito por parte de instituições financeiras de comunicar taxas proporcionais como se fossem equivalentes. Uma taxa será a nominal, a que aparece, e a outra será a efetiva, a que realmente é utilizada.
Identificar taxas nominais e levar isso em consideração na análise de um financiamento.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Porcentagem;
Fator de atualização: É importante que o aluno saiba que um capital C, aumentado de uma taxa i, fica multiplicado por (1+i). Para revisar este conteúdo recomendamos a aula:
http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=25767
Estratégias e recursos da aula
Prezado professor, em geral as instituições financeiras tem o péssimo hábito de comunicar taxas proporcionais como se fossem taxas equivalentes. Uma expressão como “12% ao ano, capitalizado mensalmente, ou com capitalização mensal” significa que a taxa usada na operação não é a taxa de 12% anunciada e sim a taxa mensal que lhe é proporcional.
Assim, a tradução da frase “12% ao ano com capitalização mensal” é “12%/12 = 1% ao mês”. Observe que 1% ao mês significa (1,01)12 – 1 = 12,68%.
Isso mesmo! Anunciam 12% mas cobram 12,68%!
Vários bancos colocam em seus contratos 12% ao ano, com capitalização mensal, e a tradução disso é que, NA VERDADE, a taxa cobrada é de 12,68% ao ano. A (falsa) taxa de 12% ao ano é chamada de taxa nominal. A taxa (verdadeira) de 12.68% ao ano é dita taxa efetiva.
Mais um exemplo:
24% ao ano com capitalização bimestral.
24%/6 = 4% ao bimestre. Isso ao ano dá 1,046 -1 = 26,5% ao ano.
Taxa nominal = 24% ao ano.
Taxa efetiva = 26,5% ao ano.
Este assunto causa uma confusão considerável, porque as taxas são apresentadas de diversas maneiras. Algumas vezes a maneira pela qual a taxa é cotada é resultado de alguma tradição, outras vezes é determinada pela legislação. Infelizmente, às vezes as taxas são cotadas de maneira deliberadamente enganosa para confundir tomadores de empréstimos e investidores.
Independente do caso, a taxa nominal é uma maneira sutil de esconder a verdadeira (efetiva) taxa cobrada na operação. Veremos algumas atividades para que os alunos tomem conhecimento da existência dessa prática, sabendo identificar as taxas nominais e descobrir as taxas equivalentes usadas nas operações de crédito.
Resumindo:
- Quando o período de formação e incorporação dos juros ao Capital não coincide com aquele a que a taxa está referida estamos diante de uma taxa nominal.
- Taxas Nominais:
- não representam os juros efetivamente pagos
- precisam ser interpretadas e devidamente convertidas para TAXAS EFETIVAS, porque são essas que correspondem aos juros efetivamente pagos
- E o mais importante: Taxas nominais são taxas proporcionais e não equivalentes!
Para saber o que são taxas equivalentes recomendamos as seguintes aulas do Portal do Professor:
- Matemática Financeira no CAp UFRJ: Equivalência de Taxas (http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=9939)
- Taxas Proporcionais e Equivalentes
ATIVIDADE 1
Um dos exemplos mais clássicos que podemos adotar para exemplificar a utilização de taxas nominais é a tradicional Caderneta de Poupança. Ela oferece atualmente ao aplicador (poupador) uma rentabilidade de 6% ao ano, capitalizados mensalmente, mais a TR. Ou seja, a poupança tem um rendimento que é definido por uma taxa nominal, pois mesmo com a TR igual a zero, a poupança não renderá 6% ao ano. Vamos ver porquê.
Nota: TR = Taxa Referencial de Juros (http://www.portalbrasil.net/tr_mensal.htm)
1) A expressão 6% ao ano, capitalizados mensalmente, significa uma rentabilidade mensal de quanto? Para responder a essa pergunta você poderá fazer uma pesquisa na internet ou perguntar para o seu professor. Uma sugestão: http://www.professordutra.com.br/blog/?p=959
2) Com a taxa encontrada no item a, determine a taxa efetiva anual, ou seja, a rentabilidade que realmente o poupador terá se deixar seu dinheiro investido por um ano, na poupança, supondo que a TR seja igual a zero.
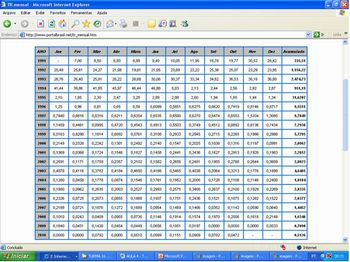
3) Agora, considere que em 2010, a TR variou conforme a tabela abaixo. Determine a rentabilidade acumulada da poupança de Janeiro a Outubro, considerando a TR de cada mês.
Tabela disponível em http://www.portalbrasil.net/tr_mensal.htm
Imagem do autor
|
|
JAN |
FEV |
MAR |
ABR |
MAI |
JUN |
JUL |
AGO |
SET |
OUT |
| 2010 |
0,5000 |
0,5000 |
0,5796 |
0,5000 |
0,5513 |
0,5592 |
0,6157 |
0,5914 |
0,5706 |
0,5474 |
| ACUMULADO |
0,5000 |
1,0025 |
1,5879 |
2,0958 |
2,6587 |
3,2327 |
3,8683 |
4,4826 |
5,0188 |
5,6540 |
ATIVIDADE 2
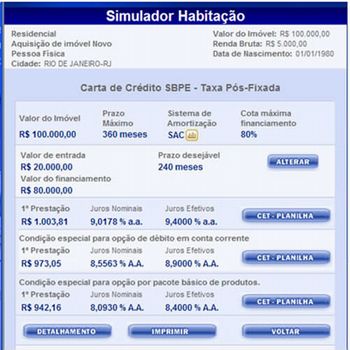
SIMULADOR DE FINANCIAMENTO HABITACIONAL - TAXAS ANUNCIADAS.
A ilustração abaixo mostra um simulador de Crédito de um determinado Banco, que concede a maioria dos financiamentos habitacionais no Brasil. João está fazendo uma simulação de um empréstimo para a compra de um imóvel. Responda as questões abaixo:
a) Qual o valor do imóvel?
b) Qual o valor que será financiado? Por que é diferente do valor do item a?
c) Ele está usando a cota máxima?
d) Há seis taxas de Juros apresentadas, dividas em dois grupos. Quais são eles?
e) Qual a diferença entre “juros nominais” e “juros efetivos”? Pesquise na Internet a diferença entre os dois.
f) Calcule os juros efetivos anuais a partir dos juros nominais anuais representados na 1ª opção do simulador.
g) Há alguma ligação entre esse cálculo e a equivalência de taxas? Explique as ligações.
h) Faça o mesmo para as outras opções.
i) Pesquise na Internet porque os juros nominais são utilizados para comunicar as taxas de operações de crédito.
Fonte: http://www8.caixa.gov.br/siopiinternet/simulaOperacaoInternet.do?method=inicializarCasoUso
ATIVIDADE 3
ANALISANDO INVESTIMENTOS.
1) Inicialmente, divida a turma em duplas;
2) Diga aos alunos que a forma como as taxas são anunciadas podem requerer uma análise mais cuidadosa na hora decidir entre investimentos.
3) Apresente aos alunos um pequeno estudo de Caso, envolvendo uma situação onde far-se-á necessária uma análise mais cuidadosa utilizando-se dos conceitos de taxas nominas e efetivas.
O CASO DOS BANCOS
| I – O banco A oferece para um investimento de R$ 200.000,00, uma taxa de 24% ao ano, capitalizados mensalmente, por um prazo de 1 ano. . . II – O banco B oferece para um investimento de mesmo valor, uma rentabilidade mensal equivalente a taxa de 18% ao ano, mais a rentabilidade mensal da poupança sem a TR. |
Lembrando que a poupança oferece atualmente ao aplicador (poupador) uma rentabilidade de 6% ao ano, capitalizados mensalmente, mais a TR, determine qual dos dois investimentos tem a melhor rentabilidade anual, justificando com cálculos sua decisão. Além disso, apresente um argumento, por escrito, apresentando para o Fernando o motivo da sugestão de investimento que vocês encontraram como a melhor!
Prezado professor. Se os alunos apresentarem dificuldades na construção do argumento, tente orientá-los na sequência apresentada abaixo. Lembre-se que é importante incentivar a investigação, procurando intervir sem retirar o prazer da descoberta. Dê as dicas abaixo aos poucos. Depois da primeira, talvez as ações seguintes possam ser percebidas e postas em prática pelos próprios alunos. Não esqueça: Intervir sem retirar o prazer da descoberta!
- Para analisar um investimento, veja as rentabilidades que cada um proporciona ao final do período acordado. Ou então, sugira para os alunos encontrarem as taxas mensais que rendem cada um dos investimentos!
- Qual o valor do dinheiro, após um ano no investimento I? Observe que a taxa de 24% é uma taxa nominal, e que precisa ser convertida. Uma vez convertida, basta levar o valor investido para daqui a um ano. Cuidado, pois a taxa obtida é mensal.
- Faça o mesmo para o Investimento II. Observe que a rentabilidade mensal da poupança é fixa e será somada à rentabilidade mensal equivalente a 18% ao ano. Ache essa taxa equivalente, some com a taxa da poupança e depois encontre a taxa equivalente anual à essa taxa mensal.
- Oriente os alunos conforme as dúvidas forem surgindo. Aqui, vão precisar utilizar todos os conceitos que já aprenderam nas aulas anteriores.
Investimento A.
A taxa mensal equivalente é 24%/12 = 2% ao mês. Essa taxa é equivalente a 1,0212 – 1 = 26,82% ao ano.
Investimento B.
A taxa mensal equivalente a 18% ao ano é (1,18)1/12- 1 = 1,39% ao mês. A poupança sem a TR rende 6%/12 = 0,5% ao mês. Logo a taxa mensal do investimento B é de 1,39% + 0,5% = 1,89% ao mês, que é menor que a taxa mensal do investimento A. A taxa anual obviamente também será menor!
Logo o investimento em A é mais rentável, sob esse aspecto.
Isso poderia ter sido concluído pensando que em A tudo é nominal, e em B, parte é equivalente. Como as duas são nominalmente iguais a 24% ao ano, B vai render menos, pois a sua taxa mensal é menor!
Recursos Complementares
Vídeos relacionados ao consumo e orçamento das famílias.
http://www.youtube.com/watch?v=51mbDDhq9gQ
Planejamento Financeiro.
http://www.youtube.com/watch?v=rp39kUJSuZg
Uma aula única de Matemática Financeira do Professor Augusto C. de O. Morgado, está disponível em http://video.impa.br/index.php?page=janeiro-de-2007. NÃO DEIXE DE ASSISTIR!!!
Portal do Professor
Matemática Financeira: O valor do dinheiro no tempo
http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=25767
Matemática Financeira no CAp UFRJ: Juros Compostos
http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=9932
Avaliação
Avaliação individual. Aplicar problemas e situações em que o aluno mostre como utilizar os conceitos apresentados para atacar e resolver situações financeiras.
Avaliação coletiva. Sugerir uma pesquisa sobre simuladores habitacionais e os tipos de taxas e seguros cobrados para quem contrai um financiamento, em diferentes bancos.
Cinco estrelas 2 classificações
- Cinco estrelas 2/2 - 100%
- Quatro estrelas 0/2 - 0%
- Três estrelas 0/2 - 0%
- Duas estrelas 0/2 - 0%
- Uma estrela 0/2 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
luciana, opet , Paraná - disse:
lulugue3@gmail.com25/03/2014
Cinco estrelasótima aula
-
zeze, Argentina - disse:
zez@ig.com.br17/09/2013
Cinco estrelasmuito bom
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus