14/02/2011
Rita Maria Cardoso Meirelles, Fernando Celso Villar Marinho, Ivail Muniz Junior, Jackson Lopes, Clayton Gonçalves Silva, Raphael Alcaires de Carvalho.
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Tecnologia para a matemática |
| Ensino Médio | Matemática | Análise de dados e probabilidade |
O que o aluno poderá aprender com esta aula
- Utilizar Excel para resolver problemas de distribuição binomial
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
- Noções de probabilidade.
Estratégias e recursos da aula
ATIVIDADE 1
ÁRVORE GENEALÓGICA
Uma árvore genealógica* é um histórico de certa parte dos ancestrais de uma pessoa ou família. Mais especificamente, trata-se de uma representação gráfica genealógica para mostrar as conexões familiares entre indivíduos, trazendo seus nomes e, algumas vezes, datas e lugares de nascimento, casamento, fotos e falecimento. O nome se dá pela semelhança em relação a ramificação de árvores.
*(http://pt.wikipedia.org/wiki/%C3%81rvore_geneal%C3%B3gica)
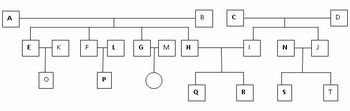
Na primeira etapa o professor deverá mostrar aos alunos como montar uma árvore genealógica. Depois cada aluno deverá fazer um estudo em sua família inserindo a geração dos avós, dos pais e a sua geração.
Imagem do autor
A árvore genealógica criada acima mostra um estudante Q e seu irmão R, cujo pai é H e a mãe é I e seus avós maternos são C e D e seus avós paternos são A e B. As letras que estão em negrito representam as pessoas do sexo masculino e as outras letras do sexo feminino. Na 1ª linha tem-se a geração dos avós, na 2ª linha a geração dos pais e na última linha a geração do aluno Q. O círculo na árvore acima significa que G e M não tem filho.
Problemas envolvendo probabilidade
Algumas questões podem ser feitas a partir da árvore acima:
1) Escolhida, ao acaso, uma das pessoas , qual a probabilidade de ser escolhido o estudante Q?
Para resolver essa questão o professor deve trabalhar os conceitos de espaço amostral e eventos. Então deve usar a fórmula de probabilidade P = (n° de elementos do evento/ n° de elementos do espaço amostral). Nessa questão, temos: P = 1/20 = 5%, pois o meu evento é ser escolhido o estudante Q para isso ocorrer só temos 1 possibilidade. E o espaço amostral é a quantidade total de pessoas presentes na árvore, ou seja, 20.
2) Escolhida, ao acaso, duas pessoas, qual a probabilidade do estudante Q ser uma dessas duas pessoas escolhidas?
O espaço amostral nesse caso é combinação de 20 tomados 2 a 2, pois podem ser escolhidas quaisquer duas pessoas, isto nós dá 190. Já para o n° de eventos o estudante Q pode ser escolhido junto com qualquer um das 19 pessoas, o que dá um total de 19 possibilidades. Portanto a probabilidade é P = 19/190 = 1/10 = 10%.
Uma outra solução é perceber que o estudante Q pode ser escolhido na 1ª escolha ou na 2ª, para a 1ª escolha temos 5% de chance para a 2ª escolha temos 5% também. Portanto, a probabilidade final é de 10%(5% + 5%).
O professor pode levar os alunos a resolver para os casos em que:
3 pessoas são escolhidas; 4 pessoas são escolhidas e assim sucessivamente.
3) Determine a probabilidade de uma pessoa escolhida ao acaso seja uma parente consaguínea de A, sabendo que não será escolhida a pessoa A?
O número de elementos do espaço amostral é 19, pois já sabemos que A não foi escolhida. O n° de elementos do evento ser consaguíneo é 8 (são: E, F, G, H, O, P, Q, R). Portanto, P = 8/19.
Recomenda-se ler o artigo no site
http://www.teliga.net/2009/06/quais-os-riscos-dos-casamentos.html
Pois envolve probabilidade e bilogia, podendo assim trabalhar a interdisciplinaridade com os aluinos.
Para estimular a curiosidade dos alunos, apresente dois sites que se propõe a auxiliar na construção de árvores geneálogicas:
http://www.myheritage.com.br/genealogia
http://www.meusparentes.com.br/centro-de-informacoes/a-arvore-genealogica
O tema "Árvore Genealógica" é abordado em aulas de Biologia. Pense na possibilidade de estabelecer um diálogo com professores desta área para tornar a aula mais abrangente. O link a seguir apresenta uma sugestão de aula de biologia sobre este tema.
http://www.educador.brasilescola.com/estrategias-ensino/arvore-genealogica.htm
A representação gráfica da árvore é chamada de heredograma. Para saber mais visite:
http://www.sobiologia.com.br/conteudos/Genetica/leismendel5.php
ATIVIDADE 2
EXCEL E GRÁFICOS
Nesta atividade o aluno deve fazer pesquisas sobre os membros da família, por exemplo, a cidade onde moram seus familiares, a idade, formação escolar, etc. Os alunos podem sugerir o que querem perguntar às famílias, essa é uma ótima fase para fazer os alunos formularem as próprias questões.
Após recolhidas as informações, deve-se colocar os dados na planilha e fazer o gráfico. Como o exemplo a seguir.
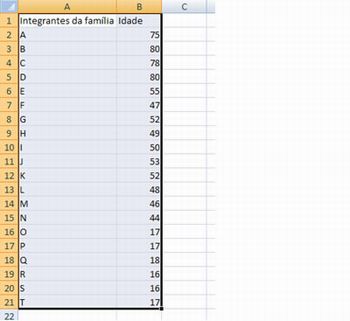
1°) Digite na planilha as informações coletadas e selecione todos os dados como mostra a figura abaixo:
Imagem do autor
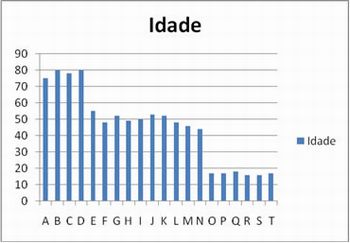
2°) No menu Inserir, selecione a opção Gráfico e depois Gráfico de Colunas.
Imagem do autor
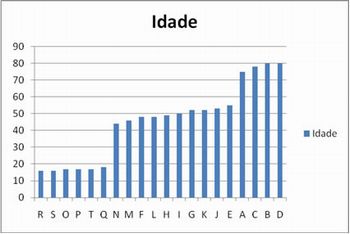
Outra possibilidade é elaborar um gráfico com as idades em ordem crescente. Para isso, primeiramente é necessário classificar os dados.
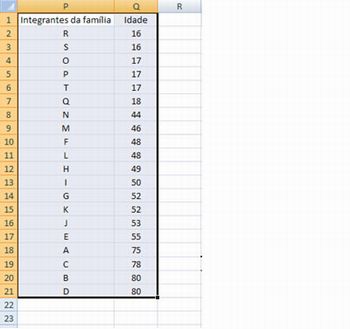
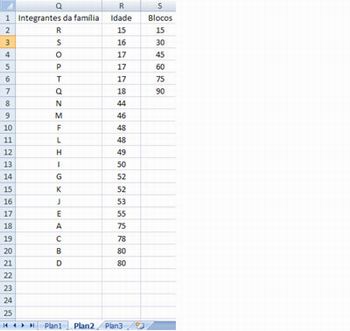
1°) Selecione todos os dados. No menu Início selecione a opção Personalizar Classificação. Na opção Classificar por selecione o parâmetro idade. Após a classificação os dados ficarão conforme a figura abaixo.
Imagem do autor
2°) No menu Inserir selecione a opção Gráfico e depois Gráfico de Colunas.
Imagem do autor
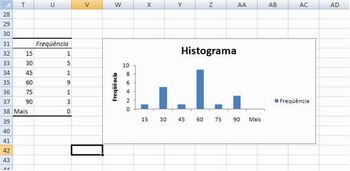
Uma terceira possibilidade é a utilização de Histograma, um gráfico que agrupa os dados em blocos e mostra a freqüência dentro de cada bloco.
1°) Coloque na coluna ao lado os blocos, nesse exemplo adotamos intervalos de 15 anos para as idades como mostra a figura.
Imagem do autor
2°) No menu Dados selecione a opção Análise de Dados e depois a opção Histograma
Imagem do autor
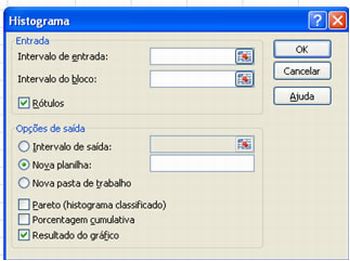
3°) No campo intervalo de entrada selecione os dados referentes às idades, células R1 a R21. No campo intervalo do bloco os intervalos escolhidos, células S1 a S7. Marque as opções Nova Planilha e Resultado do Gráfico.
Imagem do autor
ATIVIDADE 3
EXCEL E A DISTRIBUIÇÃO BINOMIAL
Esta atividade é composta de três etapas.
I) Cada aluno deverá analisar a árvore genealógica da sua família e calcular a probabilidade de escolhida ao acaso um dos membros da sua família ser homem. No nosso exemplo, de 20 pessoas, 11 são do sexo masculino. Portanto a probabilidade pedida é de 55%. Quando a probabilidade não for exata a calculadora será um instrumento para a realização do cálculo.
II) O aluno deverá resolver dois problemas:
Problema 1: “Cinco parentes, dos que estão na árvore montada acima, serão chamados de forma aleatória para participar de um evento na escola. Qual é a probabilidade de dois desses parentes serem do sexo masculino?”
Para responder tal pergunta o aluno deverá usar o conceito de distribuição binomial. Mais uma vez a turma deverá ser levada para o laboratório de informática para usar a planilha eletrônica.
O aluno deverá preencher a planilha da forma como mostra o exemplo a seguir:
Imagem do autor
Onde n é o número de pessoas escolhidas (número de tentativas), k o número de pessoas do sexo masculino que queremos calcular a probabilidade (número de sucessos), p a probabilidade de uma pessoa ser do sexo masculino (a probabilidade do sucesso) e P(X = k) a probabilidade de em um grupo de 5 pessoas 2 serem do sexo masculino.
Para calcular P(X=k) o aluno deverá clicar na célula D2 e depois clicar no botão inserir função
Imagem do autor
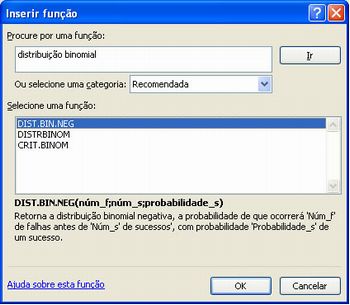
E abrirá a janela
Imagem do autor
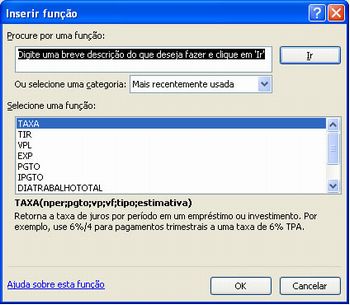
Digite distribuição binomial e clique em ir e aparecerá a tela
Imagem do autor
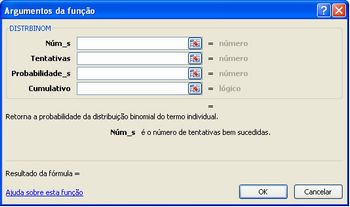
Selecione DISTRBINOM e clique em OK. E aparecerá a tela
Imagem do autor
No 1° campo digite 2, no 2° 5, no 3° 0,55 e no último falso e clique em OK. E aparecerá o resultado desejado.
Imagem do autor
Problema 2: “Cinco parentes, dos que estão na árvore montada acima, serão chamados de forma aleatória para participar de um evento na escola. Sabendo que os pais do aluno devem comparecer ao evento, qual é a probabilidade de dois desses parentes serem do sexo masculino?”
III) O professor deverá apresentar a fórmula de distribuição binomial P(X = k) = (nk)pk qn-k e pedir para o aluno resolver o mesmo problema acima só que sem usar o Excel. O aluno perceberá que em determinados momentos as contas são muito difíceis de serem efetuadas.
Recursos Complementares
Planilha Eletrônica Gratuita
Portal do Professor
Sistemas Lineares no CAp UFRJ: Resolvendo Equações Matriciais no Excel
http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=7204
Matemática Financeira no CAp UFRJ: Opções de Pagamento e Planilhas Eletrônicas
http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=13004
Avaliação
Propor situações-problemas para serem resolvidos mediante o uso da função DISTRBINOM do Excel e propor a elaboração de gráficos feitos por meio de planilhas eletrônicas. Para isso, aproveite as atividades 2 e 3.
Cinco estrelas 1 classificações
- Cinco estrelas 1/1 - 100%
- Quatro estrelas 0/1 - 0%
- Três estrelas 0/1 - 0%
- Duas estrelas 0/1 - 0%
- Uma estrela 0/1 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Vilson, N/A , São Paulo - disse:
vsfj@hotmail.com27/10/2011
Cinco estrelasMuito bom.
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus