Portal do Governo Brasileiro
Início do Conteúdo
VISUALIZAR AULA
 
Combinando Reflexões e Translações

 

17/02/2011

Autor e Coautor(es)
VICTOR CESAR PAIXAO SANTOS
imagem do usuário

RIO DE JANEIRO - RJ Universidade Federal do Rio de Janeiro

Rita Maria Cardoso Meirelles, Fernando Celso Villar Marinho, Jackson Lopes da Cunha, Raquel Cupolillo Simões de Sousa, Ivail Muniz Junior, Clayton Gonçalves Silva

Estrutura Curricular
Modalidade / Nível de Ensino Componente Curricular Tema
Ensino Médio Matemática Geometria
Ensino Médio Matemática Álgebra
Ensino Médio Matemática Tecnologia para a matemática
Ensino Médio Matemática Números e operações
Dados da Aula
O que o aluno poderá aprender com esta aula
  • Conhecer as transformações de translação e reflexão, suas principais características e propriedades;
  • Compreender o resultado da combinação das duas transformações;
  • Identificar de que modo a mudança na ordem de duas transformações pode alterar o resultado final obtido.
Duração das atividades
2 tempos de 50 minutos
Conhecimentos prévios trabalhados pelo professor com o aluno

 

Medidas de ângulos;
 
Reta Numerada;
 
Sistema de coordenadas cartesianas (eixos ortogonais).
Estratégias e recursos da aula

 

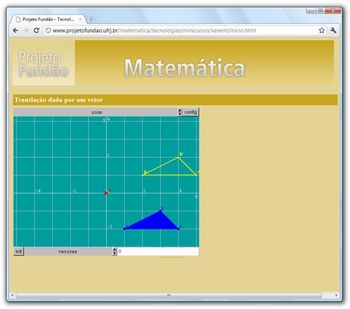
Transformações no Plano

 
Esta aula foi desenvolvida a partir de atividades propostas no  Projeto Novas Tecnologias no Ensino - Introdução às Funções Reais
 
 
Projeto Novas Tecnologias no Ensino
 
 
Uma das aplicações mais interessantes e conhecidas dos computadores são os recursos gráficos como os utilizados em projetos de computação gráfica. Geralmente, a parte mais difícil destes projetos está ligada ao problema de como desenhar e mover alguma coisa. Esta dificuldade está relacionada, em geral, ao problema geométrico de desenhar figuras como triângulos e círculos e de manipular e transformar tais figuras.
 
Para desenhar qualquer forma bidimensional, uma curva plana por exemplo, a maioria dos programas de computadores marca pontos e liga estes pontos por segmentos de retas. O que aparece na tela do computador nos dá a impressão de ser uma curva suave quando na realidade, é a união de muitos segmentos de reta bem pequenos. No caso de objetos tridimensionais, estes programas usam pequenos polígonos, em geral muitos triângulos, para que o olho do observador veja na tela uma superfície suave. Várias cenas de filmes como Jurassic Park, Vida de Inseto, Toy Story, Os Monstros foram feitas desenhando e movendo polígonos.

 

Rosto Polígonos

Fonte da Imagem: http://www.sinmec.ufsc.br/sullivann/inicio.html

 

 

Se montar a figura já é um problemão, imagine o trabalho que será movê-la! Para mover toda a figura, é necessário saber como e para onde mover cada pequeno polígono que a compõe. Porém, desde que saibamos resolver o problema mais simples de como mover um polígono, poderemos mover a figura inteira, bastanto para isso, mover um polígono de cada vez. Desse modo, para aprender a fazer animações computacionais, devemos, em primeiro lugar, aprender como animar polígonos, por exemplo, um triângulo.

 

 

 

Atividade 1

Translações

 

 

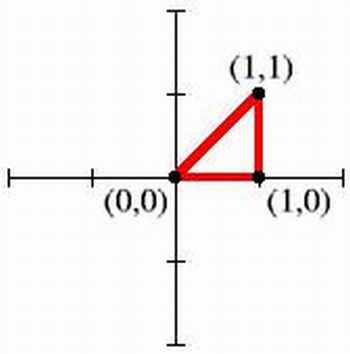
Desenhar um triângulo é muito fácil. Devemos começar definindo as coordenadas dos seus três vértices e unir estes vértices por segmentos de reta. De alguma maneira, dependendo do programa que utilizamos, devemos transmitir ao computador instruções como as que aparecem na primeira coluna da tabela abaixo, para desenhar o triângulo que aparece na segunda.
 
1) Desenhe o segmento que une os pontos (0,0) a (1,0).
2) Desenhe o segmento que une os pontos (1,0) a (1,1).
3) Desenhe o segmento que une os pontos (1,1) a (0,0).
Triângulo

http://www.im.ufrj.br/dmm/projeto/projetoc/precalculo/sala/conteudo/conteudop.htm

 
Até aí foi fácil! Dessa mesma maneira, podemos desenhar figuras mais complicadas.
 
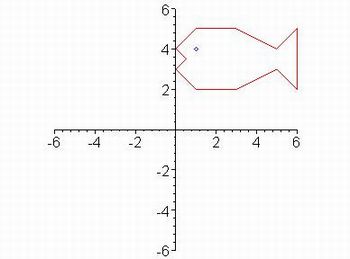
A figura ao lado foi traçada ligando-se os pontos (0,3),(1,2),(3,2),(5,3),(6,2),(6,5),(5,4),
(3,5),(1,5),(0,4),(0.5,3.5),(0,3) por segmentos de reta e marcando-se o ponto (1,4) por um pequeno losango.
Peixe

http://www.im.ufrj.br/dmm/projeto/projetoc/precalculo/sala/conteudo/conteudop.htm

 
Mas o que fazer para instruir o computador para mover o triângulo original? É claro que o que nós precisamos fazer, é fornecer ao computador a coordenada dos novos três vértices e instruí-lo a desenhar o novo triângulo e, ao mesmo tempo, apagar o triângulo original. Algumas vezes esta não é uma tarefa das mais complicadas. Mas, experimente, por exemplo, descrever, como fizemos acima, as ordens a serem transmitidas ao computador, para obter a animação abaixo! Pessoas inteligentes, ao invés de gastar horas e horas em tentativas e erros, certamente, vão preferir descobrir, estudar e fazer uso da matemática que existe por trás desse problema e, então, usar esta matemática para resolvê-lo. Afinal, sendo a geometria o ramo da matemática que estuda não somente as formas e tamanhos das figuras, mas também como manipular e transformar estas figuras, este problema deve ser resolvido usando-se algum tipo de propriedade geométrica!
 
Peixe animado
Vamos, portanto, tentar entender um pouco mais o que acontece numa animação. Uma animação feita em computador, como os desenhos animados de antigamente, consiste em vários quadros que são apresentados em uma seqüência muito rápida, nos dando a ilusão de movimento. Para automatizar o processo de animação, o computador precisa ser capaz de, automaticamente, atualizar a localização de cada objeto que se move, em cada um dos quadros que compõe a seqüência. Em outras palavras, ao receber a coordenada de um ponto, o computador precisa saber que regra especial usar para transformá-la nas coordenadas de um novo ponto. Em matemática, estas regras especiais que transformam pontos do plano em outros pontos do plano são chamadas transformações.
 
No mundo que nos rodeia, encontramos transformações a cada instante. A qualquer hora que você pegue um objeto qualquer e o mova para qualquer outro lugar, há uma transfomação geométrica que descreve o movimento da antiga posição para a nova. Entretanto, as transformações que aparecem no mundo físico são de um tipo muito especial. Não importa de que maneira você mova um caneco de cerveja, por exemplo, ele será sempre o mesmo caneco de cerveja. Em matemática ou em computação gráfica, ao contrário, se escolhermos uma transformação ao acaso, é quase certo que ela, ao mover o objeto, provocará também uma distorção na sua forma e/ou no seu tamanho.
 
Portanto, para fins de animação computacional, as transformações que são mais interessantes são aquelas que correspondem ao que no mundo físico chamamos de movimento rígido, isto é, movimentos que preservam a forma e o tamanho dos objetos. Movimentos rígidos dão origem a figuras ou objetos congruentes.
 
Em Geometria Plana, dizemos que duas figuras são congruentes se coincidirem perfeitamente, por meio de uma mudança de posição ou movimento rígido. Vamos usar o peixinho traçado acima, para ilustrar esta afirmação.
 
Em matemática, tais transformações ou movimentos são chamados de isometrias (do grego, mesma medida). Pelo exemplo anterior, é fácil concluir o porquê deste nome. Movimentos rígidos ou isometrias devem ser as transformações que preservam o comprimento dos segmentos distância e, consequentemente a distãncia entre dois pontos quaisquer do plano e na realidade, é esta a definição matemática de uma isometria.
 
Uma boa maneira de começar o nosso estudo de isometrias é pensar naquelas que nos são bastante familiares. Assim, coloque uma folha de papel alto de uma mesa e desloque-a até embaixo. A menos que você tenha amassado ou cortado a folha, neste movimento, o tamanho e a forma da folha de papel não sofreram nenhum tipo de alteração. Por isso, a sua posição final poderá e deverá ser obtida por algum tipo de isometria.
 
Pensando um pouco, podemos imaginar pelo menos quatro maneiras diferentes de mover a folha sobre a mesa. Estes movimentos são ilustrados nas animações abaixo.
 
 
Peixe animado Peixe animado Peixe animado Peixe animado
Reflexão
Translação Rotação Reflexão com Deslizamento

 

 

 

É claro que pode haver alguma outra forma de mover a folha sobre a mesa. O que acontece, por exemplo se tranladarmos a folha e depois girarmos em torno de um ponto? Como cada uma dessas transformações é uma isometria (não distorce o quadrado), a combinação das duas deve ser uma isometria também. A pergunta que devemos tentar responder é se a combinação destas duas transformações é uma isometria que está na nossa lista ou é um novo tipo de isometria que esquecemos de enumerar? Para responder a esta pergunta, precisamos conhecer um pouco mais a respeito de cada uma das transformações listadas.
 

 

 

 

1º) Faça a exposição oral com apoio de um projetor para as imagens disponíveis acima.

2º) Leve os alunos para um laboratório de informática.

3º) Apresente as informações a seguir.

 

 
A mais comum das isometrias é a chamada translação. Uma figura sofre uma translação quando se desloca, sem se deformar, paralelamente a uma direção fixada.
 
Translação
 
 
No exemplo ao abaixo o peixinho verde pode ser obtido transladando-se o vermelho na direção horizontal, 7 unidades para a direita. 
 
 

 

 

Translação do peixinho

 

4º) Agora é a vez dos alunos. Indique o site a seguir para que eles possam resolver exercícios sobre translação.
 
Atividade de Translação
 
 
 

 

Atividade 2

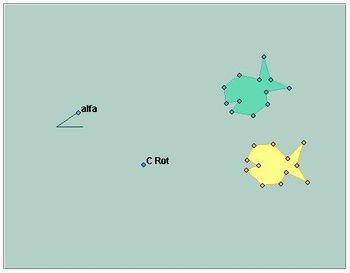
Rotações

Uma outra classe de transformações é obtida quando fixamos um ponto do plano e giramos a figura de um ângulo alpha qualquer, ao redor deste ponto.

Peixe animado                            Peixe animado

 

http://www.im.ufrj.br/dmm/projeto/projetoc/precalculo/sala/conteudo/capitulos/cap26s2.html

 

Considere, por exemplo, o triângulo cujos vértices são dados pelos pontos (1,1), (1,3), (2,1). (Figura A). Agora vamos girar esta figura. Copie a figura numa folha de papel transparente e recote-a usando a linha pontilhada como guia. Espete um alfinete na origem do sistema de coordenadas e use este alfinete para prender o recorte no desenho da Figura A, de modo que as duas figuras coincidam perfeitamente. Gire o recorte 90 graus no sentido contrário ao dos ponteiros do relógio, isto é, de tal modo que o eixo x do recorte coincida com a posição do eixo y na figura original. O triângulo do recorte deve estar agora na mesma posição do triângulo mostrado na Figura B.

 

Peixe animado Peixe animado
Figura A Figura B

 

Esta transformação é definida geometricamente como uma rotação de 90 graus em relação à origem. A animação abaixo ilustra este movimento.

 

Peixe animado

http://www.im.ufrj.br/dmm/projeto/projetoc/precalculo/sala/conteudo/capitulos/cap26s2.html

 

1º) Faça a exposição oral com apoio de um projetor para as imagens disponíveis acima.

2º) Ainda com os alunos no laboratório de informática, indique os sites abaixo para que eles possam visualizar a rotação de figuras.

 

http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/RotacaoFigura.html

 

Rotação de peixes

 

http://www.im.ufrj.br/dmm/projeto/projetoc/precalculo/sala/conteudo/capitulos/Rot2.htm

 

 

Atividade 3

 

 

Reflexões Axiais

 
 
Dizemos que duas figuras são simétricas em relação a uma reta qualquer quando uma é a imagem espelhada da outra em relação à reta considerada, chamada eixo de simetria. Isto quer dizer que se desenharmos as figuras numa folha de papel e dobrarmos o papel de tal modo que a dobra coincida com a reta em questão, as duas figuras coincidirão perfeitamente. Isto acontece porque pontos simétricos estão em lados opostos, mas à mesma distância do eixo de simetria, isto é, o eixo de simetria é a mediatriz do segmento de reta que une estes dois pontos.
Reflexão dos Peixes
 
 
Os peixinhos da figura acima são simétricos em relação ao eixo y . Neste caso, dizemos que o peixinho vermelho sofreu uma reflexão ou que foi refletido em relação ao eixo y . Dizemos também, que o peixinho verde pode ser obtido a partir do vermelho, por meio de uma reflexão em relação ao eixo y .
 
Logo importante
 
A transformação de Reflexão Axial também é conhecida como Simetria Axial.

 

1º) Faça a exposição oral com apoio de um projetor para as imagens disponíveis acima.

2º) Ainda com os alunos no laboratório de informática, indique os sites abaixo para que eles possam visualizar a reflexão de figuras.

Simetria

http://www.projetofundao.ufrj.br/matematica/tecnologias/minicursos/xenem/SimetriaAxial.html

 

 

Atividade Extra

 

Combinando Reflexões & Translações

Como já vimos, transformações podem ser combinadas. Isto é feito executando-se várias transformações em seqüência. Neste caso, a ordem em que as transformações são executadas é importante no resultado final. Nesta atividade vamos explorar a combinação de reflexões e translações.

 

Indicamos que o professor acesse o site: http://www.im.ufrj.br/dmm/projeto/projetoc/precalculo/sala/conteudo/capitulos/reflexn3.htm e manipule os objetos para mostrar como podem ser combinadas as transformações de Reflexão e translação.

 

 

 

Recursos Complementares
Avaliação

Como avaliação individual sugerimos a atividade disponível no link:

http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/ExerAula5Rotação.pdf

Outras ideias para questões podem ser retiradas da lista de exercícios disponível em

http://www.cap.ufrj.br/matematica/PortaldoProfessorMec/atividades/Atividades_rotacao.pdf

Opinião de quem acessou

Quatro estrelas 2 classificações

  • Cinco estrelas 1/2 - 50%
  • Quatro estrelas 1/2 - 50%
  • Três estrelas 0/2 - 0%
  • Duas estrelas 0/2 - 0%
  • Uma estrela 0/2 - 0%

Denuncie opiniões ou materiais indevidos!

Opiniões

  • Marcelo Silva, EMIEF JOAO BAPTISTA ORTIZ MONTEIRO , São Paulo - disse:
    marcelosilva.alfa@gmail.com

    09/12/2015

    Quatro estrelas

    Trabalho muito bom e dinâmico para os alunos. Parabéns professor

  • SAMUEL DE SOUSA SILVA, Secretaria Municipal de Educação de TERESINA , Piauí - disse:
    samuel.mat@hotmail.com

    10/05/2011

    Cinco estrelas

    muito interessante, pois nada como a computação para conseguir uma demonstração tão maravilhosa!

Sem classificação.
REPORTAR ERROS
Encontrou algum erro? Descreva-o aqui e contribua para que as informações do Portal estejam sempre corretas.
CONTATO
Deixe sua mensagem para o Portal. Dúvidas, críticas e sugestões são sempre bem-vindas.