A fim de desenvolver competências da área 5 da Matriz de Referência Matemática e suas Tecnologias do ENEM, que é Modelar e resolver problemas que envolvem variáveis socioeconômicas ou técnico-científicas, usando representações geométricas, bem como a interpretação de gráfico cartesiano que represente relações entre grandezas (H20) e ainda a utilização de conhecimentos algébricos/geométricos como recursos para a construção de argumentação (H22), são propostos para esta aula os seguintes objetivos:

• Estudar o sinal da função tangente em cada um dos quadrantes.
• Verificar em quais intervalos a função tangente é crescente e em quais é decrescente.

4 horas/aula (50 minutos cada).

• Plano cartesiano e suas características: eixos, origem e quadrantes.
• O Círculo (ou ciclo) Trigonométrico.
• Definição da função tangente no círculo trigonométrico.

Esta aula é continuação das aulas:

 

Estudando o círculo (ou ciclo) trigonométrico com o software GeoGebra – Parte 1: propriedades e determinação do cosseno. Disponível em http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=55745, acesso em 06 de Junho de 2014.

 

Estudando o círculo (ou ciclo) trigonométrico com o software GeoGebra – Parte 2: Propriedades do cosseno em cada um dos quadrantes. Disponível em:

http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=55761, acesso em 06 de Junho de 2014.

 

Estudando o círculo (ou ciclo) trigonométrico com o software GeoGebra – Parte 3: determinação do seno no ciclo trigonométrico. Disponível em: http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=55788, acesso em 06 de Junho de 2014.

 

Estudando o círculo (ou ciclo) trigonométrico com o software GeoGebra –

Parte 4: Propriedades do seno em cada um dos quadrantes. Disponível em: http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=56417, acesso em 13 de Julho de 2014.

 

Estudando o círculo (ou ciclo) trigonométrico com o software GeoGebra – Parte 5: Definindo a tangente no ciclo trigonométrico. Disponível em: http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=56740 , acesso em 23 de Julho de 2014.
 

 

Todas disponíveis no Portal do Professor.

 

Comentário: Essa aula deve ser desenvolvida em um laboratório de informática com um computador por aluno ou em dupla, para possibilitar a interação e acompanhamento das atividades pelos alunos.

 

O Software GeoGebra – Apresentação:

Nesta aula, o círculo (ou ciclo) trigonométrico será estudado com o auxílio do software GeoGebra. Segundo Humberto José Bortolossi(s.d.), o GeoGebra, criado por Markus Hohenwarter, é um software gratuito de matemática dinâmica desenvolvido para o ensino e aprendizagem da matemática nos vários níveis de ensino (do básico ao universitário). O GeoGebra reúne recursos de geometria, álgebra, tabelas, gráficos, probabilidade, estatística e cálculos simbólicos em um único ambiente. Assim, o GeoGebra tem a vantagem didática de apresentar, ao mesmo tempo, representações diferentes de um mesmo objeto que interagem entre si.

O software encontra-se disponível para download no site <http://www.baixaki.com.br/download/geogebra.htm>, acesso em 13 de abril de 2014.

 

Figura 1: Apresentação do Software GeoGebra.

 

Fonte: Arquivo do autor.

 

PRIMEIRO MOMENTO: Analisando o comportamento da tangente em função da variação do ângulo central da circunferência.

 

Professor (a), inicialmente, solicite aos alunos que construam o ciclo trigonométrico e um ponto C sobre o círculo.

 

Comentário: A construção do círculo trigonométrico e a definição da função tangente podem ser encontradas nas aulas:

Estudando o círculo (ou ciclo) trigonométrico com o software GeoGebra – Parte 1: propriedades e determinação do cosseno, disponível em http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=55745, acesso em 06 de Junho de 2014.

 

Estudando o círculo (ou ciclo) trigonométrico com o software GeoGebra – Parte 5: Definindo a tangente no ciclo trigonométrico, disponível em http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=56740, acesso em 23 de Julho de 2014.
 

 

Disponíveis no Portal do Professor.

 

Em seguida, peça aos alunos que exibam o ângulo 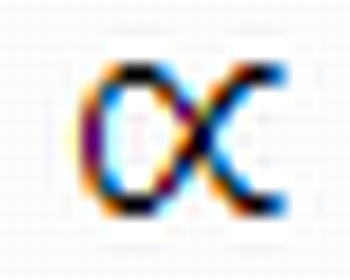descrito pelo arco BC e que, então, construam o segmento  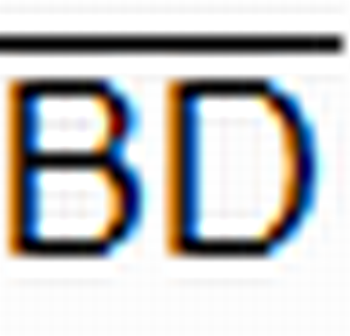que representa a tangente deste ângulo, conforme está explicado na aula citada anteriormente.

 

Figura 2: ângulo 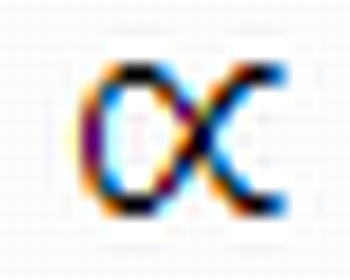e o segmento 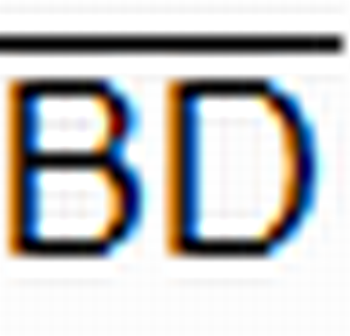que representa sua tangente.

 

 

 

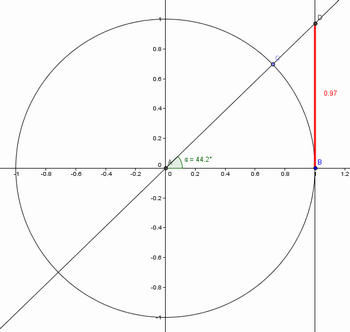
Fonte: Arquivo do autor.

 

Observação: Relembre com os alunos que para destacar o segmento, basta clicar com o botão direito sobre o segmento e selecionar a opção Propriedades dos Objetos. Abrirá a seguinte janela (figura 3).

 

Figura 3: Propriedades dos Objetos.

 

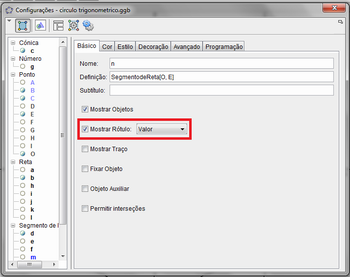
Fonte: Arquivo do autor.

 

Na aba básico, peça para selecionarem a opção Mostrar Rótulo e, na caixa ao lado, a opção Valor. Além disso, os alunos poderão mudar a cor do segmento (na aba Cor) e a espessura do objeto (na aba Estilo). Após fazer as alterações (figura 2), basta que feche a janela para que sejam realizadas.

 

Comentário: O comprimento do segmento é exibido ao lado do próprio objeto.

 

Professor (a), peça para os alunos selecionarem a opção Mover na barra de ferramentas (figura 4), e em seguida clicar sobre o ponto C e movimentá-lo ao longo da circunferência. Deixe que os alunos manuseiem essa ferramenta e que discutam o que estão percebendo que ocorre quando movimentam o ponto sobre a circunferência. Em seguida, apresente-lhes algumas questões e peça-lhes para que registrem as respostas.

 

Figura 4: Como mover um objeto no GeoGebra.

 

 

 

Fonte: Arquivo do autor.

 

Comentário: O registro pode ser realizado tanto no caderno, quanto em um editor de texto, como por exemplo, o Word da Microsoft.

 

QUESTÕES

 

(A) ÂNGULO NULO E PRIMEIRO QUADRANTE

 

Peça para que os alunos posicionem o ponto C coincidindo com (1, 0), como mostra a figura 5. Então questione.

 

Figura 5: Tangente de 0º.

 

 

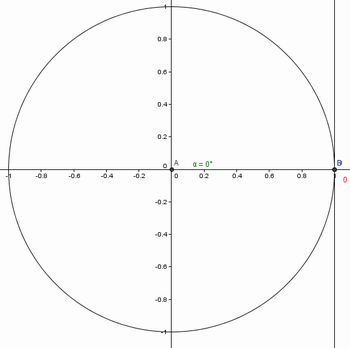
Fonte: Arquivo do autor.

 

1)      Qual é a medida do ângulo 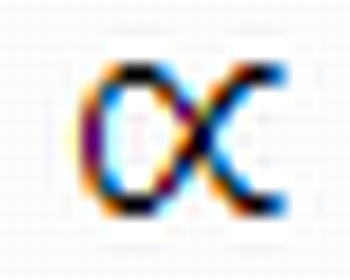quando o ponto C encontra-se nesta posição? Qual o valor da tangente deste ângulo?

Espera-se que os alunos, ao observarem a medida apresentada no círculo, pelo software, percebam que neste ponto, a tangente mede zero (0).

 

Peça para os alunos movimentarem o ponto C lentamente no sentido anti-horário (em direção ao ponto (0,1)), mas apenas enquanto o ângulo 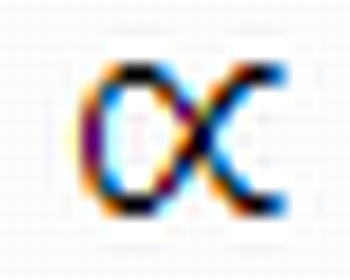for menor do que 90º (figura 6).

 

Figura 6: Variando a tangente no primeiro quadrante.

 

 

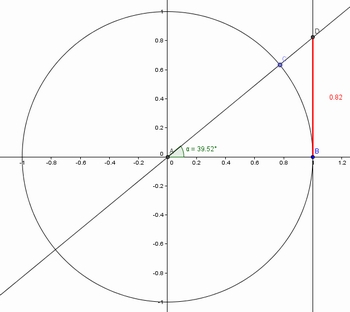
Fonte: Arquivo do autor.

 

2)      Qual o sinal da tangente deste ângulo, quando o ponto C está no primeiro quadrante?

Resposta esperada: No primeiro quadrante, o sinal da tangente é positivo.

 

3)      O que está acontecendo com a tangente quando aumentamos o ângulo?

Espera-se que os alunos percebam que, à medida que o ângulo aumenta de 0º para 90º, a tangente sempre aumenta.

 

4)      Aumenta “de quanto para quanto”?

Espera-se que os alunos percebam que aumenta de zero (0) e infinitamente.

 

 

Observação: Podem surgir algumas dúvidas pelo fato de só ser possível ver o ponto D , também, a medida do comprimento do segmento até certa altura. A partir de então, o aluno não consegue mais o ver. Neste caso, é interessante que se peça para os alunos posicionarem o ponto C mais próximo de (0,1) e reduzir a imagem e arrastando-a até encontrar a medida do comprimento. Solicite aos alunos para irem aproximando cada vez mais o ponto  C de (0 ,1) e que repita o procedimento de reduzir e arrastar para encontrar a medida do comprimento, em seguida, questionar:

 

 

5)      Em algum momento a tangente vai parar de aumentar?

Espera-se que os alunos percebam que por mais que aproximemos C de (0,1), a medida do comprimento de 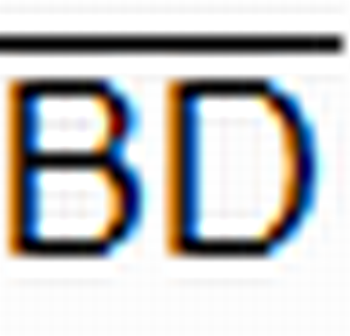 não irá parar de aumentar.

 

 

(B)  ÂNGULO RETO

 

Após todos compreenderem, peça para que posicionem o ponto C sobre o ponto (0,1) (figura 7).

 

Figura 7: Tangente de 90º.

 

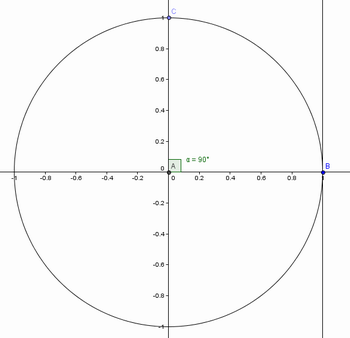
Fonte: Arquivo do autor.

 

6)      Qual a medida do ângulo 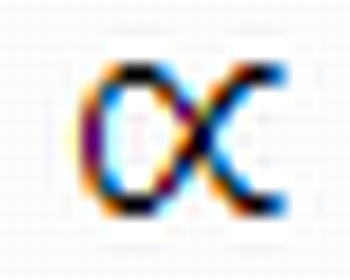? Qual o valor da tangente deste ângulo?

Os alunos irão identificar que no ângulo 90º e o segmento 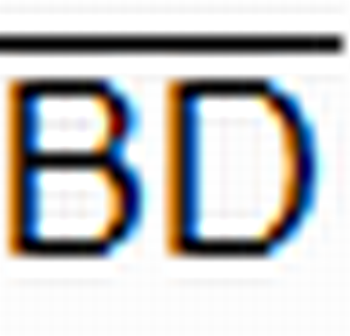 , que é a tangente de 90º,  desaparece.

 

7)      Por que o segmento desapareceu? Onde está localizado o ponto D?

Espera-se que os alunos percebam que não existe o ponto D, pois ele é a intersecção da reta x = 1 e a reta que passa pela origem e o ponto C que, neste caso, serão paralelas.

 

Caso haja alguma dúvida, destaque para os alunos que ambas as retas são perpendiculares ao eixo x, sendo assim paralelas. Portanto, não há intersecção entre elas. Assim, a tangente de 90º não existe.

 

 

(C) SEGUNDO QUADRANTE

 

Em seguida, peça para os alunos moverem o ponto C lentamente ao longo do segundo quadrante, sem que o mesmo chegue ao ponto (-1,0).

 

Figura 8: Tangente no segundo quadrante.

 

 

 

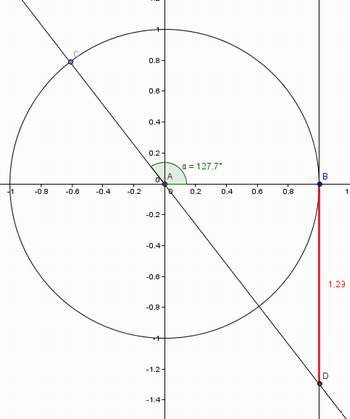
Fonte: Arquivo do autor.

 

 

Então volte a questionar.

 

8)      O ponto D encontra-se acima ou abaixo do eixo x? O que isso quer dizer?

É esperado que os alunos percebam que o ponto D esta abaixo do eixo x e portanto a tangente é negativa neste ponto.

 

9)      A tangente é negativa em todos os pontos do segundo quadrante?

 

Caso seja necessário peça para eles irem aproximando o ponto C do ponto (-1,0) para verem que a tangente será sempre negativa.

 

10)  Qual a variação da tangente no segundo quadrante?

Espera-se que os alunos percebam que quanto mais próximo o ponto está do ponto (0,1), mais abaixo está o ponto D e menor será a tangente. Assim, a tangente varia de menos infinito, até 0.

 

 

(D) ÂNGULO RASO

 

Em seguida, peça para os alunos posicionarem o ponto C sobre o ponto (-1,0) (figura 9).

 

Figura 9: Tangente de 180º.

 

 

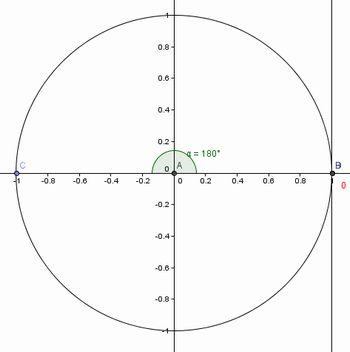
Fonte: Arquivo do autor.

 

11)  Qual a medida do ângulo central quando o ponto C encontra-se nesta posição? Qual o valor da tangente deste ângulo?

Os alunos devem perceber que a tangente de 180º é 0, já que os pontos    B e D coincidem sobre o eixo x.

 

 

(E)  TERCEIRO QUADRANTE

 

Em seguida, peça aos alunos para moverem o ponto C lentamente ao longo do terceiro quadrante, sem que o mesmo chegue ao ponto (0, -1).

 

Figura 10: Tangente no terceiro quadrante.

 

 

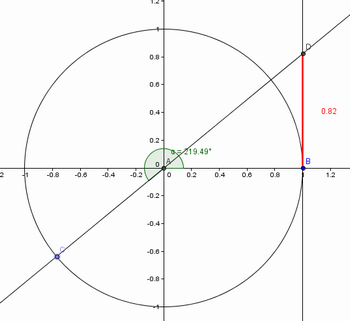
Fonte: Arquivo do autor.

 

12)  Qual o sinal da tangente no terceiro quadrante?

Espera-se que os alunos percebam que o sinal é positivo, uma vez que a intersecção está acima do eixo x.

 

13)  A medida que aumentamos o valor do ângulo de 180º para 270º, o que acontece com a tangente?

Espera-se que os alunos observem que, quando aumentamos o ângulo de 180º para 270º, a tangente vai aumentando infinitamente, como ocorre quando aumentamos de 0º para 90º, já que as retas “coincidirão”.

 

 

(F)  3/4 DA CIRCUNFERÊNCIA

 

Professor (a), solicite aos alunos que posicionem o ponto C sobre o ponto (0,-1) (figura 11).

 

Figura 11: Tangente de 270º.

 

 

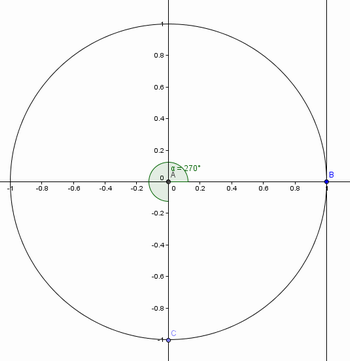
Fonte: Arquivo do autor.

 

14)  Qual a medida do ângulo quando o ponto C encontra-se nesta posição? Qual o valor da tangente?

Os alunos devem perceber que a tangente de 270º não existe, como no caso de 90º, pois a as retas são paralelas e, portanto, não há intersecção.

 

 

(G) QUARTO QUADRANTE

 

Neste momento, os alunos devem mover o ponto C lentamente ao longo do quarto quadrante, sem que o mesmo chegue no ponto (1,0).

 

Figura 12: Tangente no quarto quadrante.

 

 

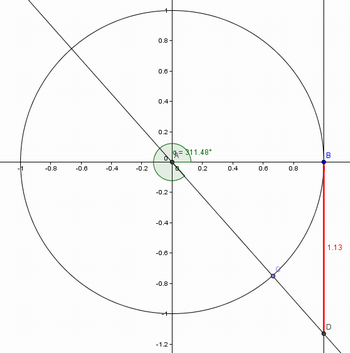
Fonte: Arquivo do autor.

 

15)  Qual o sinal da tangente no quarto quadrante?

Os alunos devem perceber que a tangente no quarto quadrante é negativa, como no segundo quadrante, pois a intersecção está abaixo do eixo x.

 

16)  O que está acontecendo com a tangente do ângulo à medida que o aumentamos de 270º para 360º?

 

Espera-se que os alunos percebam que ao variarmos o ângulo entre 270º e 360º, a tangente assume valores negativos de menos infinito a zero (0), como ocorre no segundo quadrante, já que as retas “coincidem”.

 

Professor (a), para finalizar e após a socialização dos registros, apresente as seguintes questões:

 

• Qual é o comportamento da tangente, quando C completa uma volta, ou seja o ângulo é maior do que 360º?
• Se C completar um ou mais giros, o que se observa em relação ao valor das tangentes?
• A tangente de um ângulo pode assumir valor máximo? E mínimo? Justifique a resposta.

 

Espera-se que os alunos verifiquem que aos passar do ponto (1,0), ou seja, completar um giro superior a 360º, o resultado volta a se repetir. Assim, dado um ângulo superior a 360º, para analisarmos sua tangente, basta analisarmos seu correspondente entre 0º e 360º (neste caso, seu correspondente seria o resto da sua divisão por 360º). Espera-se também que eles percebam que a tangente não assume valor máximo, pois posicionando o ponto C no primeiro quadrante e cada vez mais próximo do ponto (0,1), a tangente é cada vez maior. Da mesma forma, a tangente não assume valor mínimo, já que ao posicionarmos o ponto C, por exemplo, no segundo quadrante e cada vez mais próximo do ponto (0,1), a tangente fica cada vez menor.

 

 

Observação: Para uma melhor visualização do resultado acima, peça para os alunos ampliar a imagem do ciclo trigonométrico, quanto mais ampliar, melhor pode ser a aproximação. O comprimento do segmento 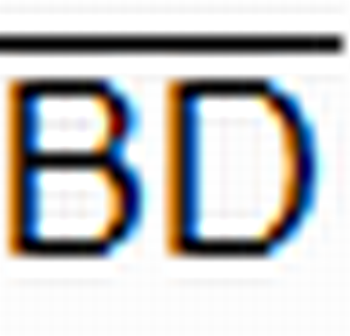, em módulo, pode ser visualizado na janela no lado esquerdo da tela (Folha Algébrica).

 

 

Comentário: É interessante relembrar com os alunos que a tangente foi definida anteriormente como sendo a razão entre o seno e o cosseno. Então volte a questionar:

 

17)  Quando definimos tangente = seno / cosseno, é sempre possível calcular essa tangente?

Espera-se que os alunos percebam que não é possível, já que nos pontos onde o cosseno é zero, não podemos fazer a divisão acima, e esses pontos são exatamente quando o ângulo é 90º + n*360º ou 270º + n*360º onde n é um número inteiro. Portanto, esta é outra maneira de verificar que a tangente não existe nos pontos referidos anteriormente.

 

 

SEGUNDO MOMENTO: Atividades de contextualização.

 

Algumas sugestões de atividades:

 

1-      Calcule o valor da tangente dos seguintes ângulos:

a)      30º                  b) 45º              c) 60º              d) 90º

 

2-      Estabeleça uma relação de comparação para:

a)      A tangente de 30º e a tangente de 60º.

b)      A tangente de 89º e a tangente de 91º.

c)      A tangente de 45º e o seno de 45º.

d)     A tangente de 300º e o seno de 30º.

 

3-      Marque V para as alternativas verdadeiras e F para as alternativas falsas.

 

(     ) Sabendo que a tangente de um ângulo é positiva, este ângulo obtuso.

(     ) As tangentes de 0º e 180º não existem.

(     ) No terceiro quadrante a tangente varia de -1 a 1.

(     ) A tangente é positiva apenas no primeiro quadrante.

(     ) Quanto mais aproximamos o ângulo de 270º, com valores menores que 270º, a tangente é cada vez maior.

(     ) Apenas no primeiro quadrante, o seno, o cosseno e a tangente têm o mesmo sinal.

Para conhecer o círculo trigonométrico:

Ciclo trigonométrico. Disponível em: http://educador.brasilescola.com/estrategias-ensino/circulo-trigonometrico.htm, acesso em 11 de maio de 2014.

Ciclo trigonométrico – Trigonometria. Disponível em:http://guiadoestudante.abril.com.br/estudar/matematica/circulo-trigonometrico-trigonometria-677843.shtml, acesso em 11 de maio de 2014.

 

Para conhecer os valores do seno, cosseno e tangente no ciclo trigonométrico:

Ciclo trigonométrico online. Disponível em: http://odin.mat.ufrgs.br/usuarios/bruno/CONDIGITAL_Cruzeiro_sul/circulo_trigonometrico/, acesso em 16 de maio de 2014.

A avaliação deverá ser feita de modo contínuo, cumulativa e sistemática em todo o processo, observando a participação efetiva do aluno, individualmente ou da dupla nas atividades propostas.

O professor poderá também adotar como critério para avaliação:

• O envolvimento do aluno com as atividades;
• A motivação em apresentar suas respostas para a turma;
• A seriedade para a correção dos exercícios.