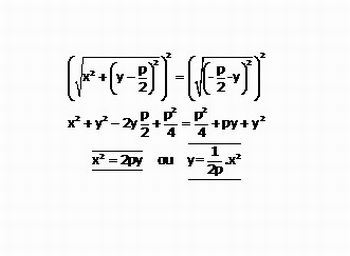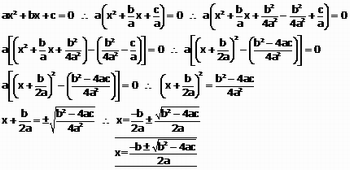06/12/2010
Rita Maria Cardoso Meirelles, Ivail Muniz Junior, Fernando Celso Villar Marinho, Jackson Lopes, Clayton Gonçalves Silva.
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Tecnologia para a matemática |
| Ensino Médio | Matemática | Álgebra |
O que o aluno poderá aprender com esta aula
A contextualização histórica que permeia o tema.
Aplicações da função quadrática no cotidiano.
Manipular gráficos utilizando o Software Nippe Descartes para explorar as formas de apresentação da função e suas características.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Distância entre dois pontos
Fatoração
Valor Absoluto ou módulo
Estratégias e recursos da aula
Professor, para realizar essa aula, encaminhe primeiramente os alunos ao laboratório de Informática, e peça que se acomodem em, no máximo, três alunos por computador.
História e a função quadrática:
O artigo Por que os nomes elipse, parábola e hipérbole? visa mostrar, de maneira interessante para a turma, a origem de cada uma. Acesse o recurso do portal: http://portal.mec.gov.br/seb/arquivos/pdf/EnsMed/expensmat_3_3.pdf e faça as adaptações para se adequarem à realidade da sua sala de aula.
Obs. Este é o primeiro artigo deste arquivo.
Figura 1: Imagem editada pela autora a partir de http://portal.mec.gov.br/seb/arquivos/pdf/EnsMed/expensmat_3_3.pdf
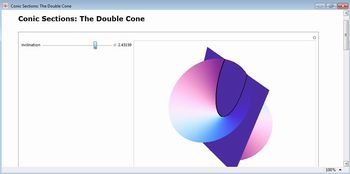
Através das simulações cujos links estão abaixo a turma visualizará que a parábola é gerada ao intersectarmos o cone com um plano paralelo à sua geratriz.
Acesse: 1 . http://demonstrations.wolfram.com/ConicSectionsTheDoubleCone
2 . http://demonstrations.wolfram.com/IntersectingARotatingConeWithAPlane
Figura 2: Imagem editada pela autora a partir de http://demonstrations.wolfram.com/ConicSectionsTheDoubleCone
Peça para a turma acessar http://www.uff.br/cdme/conicas/index.html e trabalhe as atividades 4 e 5 deste site, referentes a parábola.
Figura 3: Imagem editada pela autora a partir de http://www.uff.br/cdme/conicas/index.html
Reserve aproximadamente 20 minutos para esta parte da aula.
A ligação entre as parábolas e as antenas parabólicas, é mostrada no artigo Por que as antenas são parabólicas?. Além desta conexão também são mostrados outros exemplos, tais como os espelhos dos telescópios e dos faróis dos automóveis. Acesse o recurso do portal: http://portal.mec.gov.br/seb/arquivos/pdf/EnsMed/expensmat_3_3.pdf e faça as adaptações para se adequarem à realidade da sua sala de aula.
Obs. Este é o segundo artigo deste arquivo.
Figura 4: Imagem editada pela autora a partir de http://portal.mec.gov.br/seb/arquivos/pdf/EnsMed/expensmat_3_3.pdf
Solicite que a turma reflita sobre o mundo à sua volta e resgate outras situações do cotidiano onde a função quadrática é utilizada, promovendo a seguir uma troca de ideias sobre o tema.
Peça que os alunos acessem a Internet e pesquisem. Deixe que eles explorem por um tempo de aproximadamente 15 minutos. Em seguida, estabeleça um momento para que cada aluno (ou grupo) exponha a pesquisa feita.
De forma a dinamizar o seu trabalho, acesse previamente o link http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/FQuadrAluno.pdf. Tire cópias do arquivo e distribua um exemplar para cada aluno. Este arquivo contém todo o material necessário ao desenvolvimento da aula.
Os alunos desenvolverão o encaminhamento para os resultados no caderno.
Reserve em torno de 15 minutos para as atividade de 1 a 6 e 25 minutos para a atividade 7.
Nesta aula você poderá utilizar outra ferramenta para facilitar o entendimento da sua turma, trata-se do software Nippe Descartes, cujas atividades propostas promovem a interação com o objeto de estudo.
Nota: As informações sobre este software estão nos Recursos Complementares.
Atividade 1:
Dedução da equação da parábola de vértice na origem do sistema cartesiano
Professor, utilize o conceito de distância já trabalhado no artigo Por que as antenas são parabólicas? na parte de interdisciplinariedade, para desenvolver no quadro de giz, junto com a turma, o raciocínio que leva à equação da parábola.
Para esta dedução consideraremos o eixo de simetria da parábola coincidente com o eixo Ox.
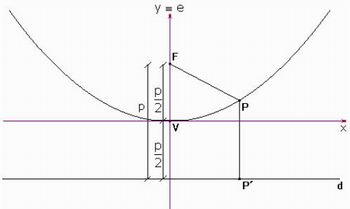
Considere P = (x, y), F = (0, p/2) e P’ = (x, -p/2). Temos, D(P,F)=d(P,P’).
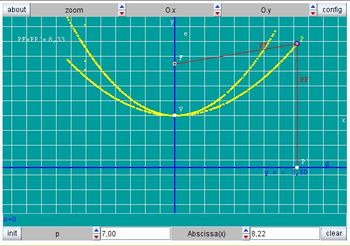
Figura 5: Dedução da equação e gráfico da parábola-Imagem da autora
Os resultados acima representam a equação da parábola de vértice na origem e eixo de simetria coincidente com o eixo dos y. Observe que comparando com a lei de formação dada inicialmente temos que a=1/(2p), portanto a parábola pode ser representada também como y=ax2.
Atividade 2:
Estudo da variação do coeficiente a na equação y=ax2
Utilize a atividade abaixo objetivando fazer com que o aluno perceba a influência da variação do coeficiente a no gráfico da função quadrática.
Peça aos alunos que acessem o link http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/FunQuadr2.html e iniciem a atividade.
Figura 6: Coeficiente a - Imagem da autora
Permita a eles manipular, fazer descobertas e responder aos questionamentos.Verifique então as respostas dadas pela turma.
a) a > 0 - concavidade voltada para cima a < 0 - concavidade voltada para baixo
b) A parábola se degenera, isto é, se transforma numa reta.
c) Conforme os valores do módulo, ou valor absoluto, de a aumentam, a abertura da concavidade da parábola vai diminuindo.
d) Quando os valores de a aumentam os de p diminuem, diminuindo também a distância entre o foco e a diretriz. O efeito que isto produz é a parábola “fechar”. Quando os valores de a diminuem, os de p aumentam, aumentando também a distância entre o foco e a diretriz. O efeito que isto produz é a parábola “abrir”.
Atividade 3:
Explorando o software para visualizar as características de uma função quadrática
Sugerimos que a parábola, representação gráfica da função quadrática, seja apresentada a partir da representação de seus elementos no plano cartesiano.
Utilize a atividade abaixo para construir com a turma a definição de parábola observando suas características através da interação com a cena dada.
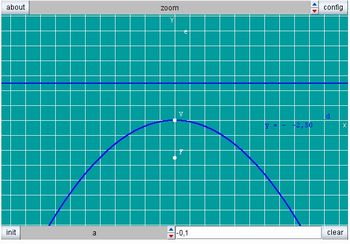
Figura 7: Parábola - Definição - Imagem da autora
Para realizar esta atividade acesse: http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/FunQuadr1.html
Uma forma de representar a função quadrática f real: é f(x)= ax2 +bx+c para todo x real onde a, b, c também reais são constantes com a ≠ 0. O lugar geométrico dos pontos que satisfazem a lei de formação da função definida anteriormente é uma Parábola.
a) O rastro deixado formará o lugar geométrico em questão.
b) A relação que deve ser encontrada é d(F,V)=d(V,d)=p/2
c) O valor de p deve ser zero (p=0).
d) Observe que p não deve ser zero, pois caso o fosse, a parábola se degeneraria, isto é, se transformaria numa reta.
e) A equação da reta diretriz é dada por d=-p/2.
f) O eixo da parábola e a diretriz são perpendiculares.
g) A parábola é simétrica em relação ao seu eixo, por este motivo podemos nos referir a esta reta como eixo de simetria da parábola.
Comentário: Depois desta atividade a turma já é capaz de formalizar o conceito de parábola.
Definindo Parábola: Professor, apresente utilizando o Data Show, uma definição de parábola.
Consideremos um plano, uma reta d e um ponto F não pertencente a d.
A parábola é o lugar geométrico dos pontos eqüidistantes de F e d, sendo F não pertencente a d.
Logo, P eqüidista de F e d, isto é, d(F,P)=d(P,d), P pertence à parábola.
Conclua esta etapa mostrando que o vértice é o ponto de interseção da parábola com seu eixo de simetria e também que o mesmo é o ponto mais próximo da diretriz.
Atividade 4:
Estudo da variação do coeficiente b na equação ax2+bx
Solicite a turma que acesse o link abaixo para iniciar a atividade: http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/FunQuadr3.html
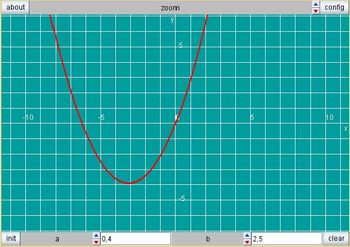
Figura 8: Coeficiente b - Imagem da autora
Comentário: Professor, caso se faça necessário antes de chegar neste último resultado estimule a turma a experimentar diferentes valores para os coeficientes a e b.
Deixe que eles a explorem e em seguida, questione sobre as descobertas feitas pela turma, verificando se os alunos apreenderam, com êxito, os conceitos trabalhados.
a) i) a=1; b=0. ii) a=1; b=1. iii) a=1; b= - 4. iv) a= -1; b=3.
b) O gráfico sofre quando a é positivo:
- Uma translação horizontal para esquerda, quando b é positivo;
- Uma translação horizontal para direita, quando b é negativo.
c) O gráfico sofre quando a é negativo:
- Uma translação horizontal para direita, quando b é positivo;
- Uma translação horizontal para esquerda, quando b é negativo.
d) Esta função translada duas unidades para a direita e 4 unidades para baixo.
e) A translação horizontal é dada por –b/2a e a vertical por f(-b/2a).
Atividade 5:
Forma Fatorada f(x)=(x-m)(x-n)
Peça a turma que acesse o link http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/FunQuadr4.html
e inicie a atividade.
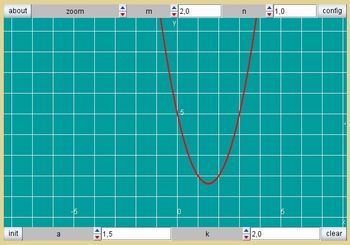
Figura 9: Imagem da autora
Comentários: Neste momento podemos transmitir para a turma que estes dois valores de x são conhecidos como raízes da equação.
Professor, peça a turma para desenvolver nesta atividade, o item 3 da letra a para perceber como o coeficiente c é obtido e sua influência no gráfico. A turma deve concluir que para encontrar a ordenada do vértice, basta substituir a abscissa do vértice na lei de formação da função.
Estimule os alunos a manipular, fazer descobertas e responder aos questionamentos. Verifique então as respostas dadas pelo eles.
a) i) a=1; m=-1; n=2; k=0. ii) a=2; m=-1; n=2; k=0. iii) a=2; m=-1; n=2; k=1.
b) Representam os valores de x onde f(x)=y=0, isto é, são os valores das abscissas onde a função corta o eixo x.
c) A abscissa do vértice é o ponto médio de m e n, ou seja, xv=(m+n)/2 .
d) Quando multiplicamos a lei de formação da função por um número positivo k, a abertura da parábola irá variar proporcionalmente (k.a), assim como a translação vertical (k.c). Quando multiplicamos a lei de formação da função por um número real negativo, a abertura da parábola continuará variando proporcionalmente, porém a concavidade da mesma irá se voltar para baixo, além disso também continuará havendo uma translação vertical, porém no sentido oposto. Em ambos os casos as translações horizontais são preservadas.
Atividade 6:
Forma Canônica
Utilizando a idéia de completamento de quadrados, iremos encontrar a fórmula para resolução da equação do 2º grau. Observe que toda equação do segundo grau pode ser escrita da forma ax2 +bx +c = 0 , com a>0. Daí:
Figura 10: Completamento de quadrados - Imagem da autora
Aplique este procedimento ao item 3 trabalhado na letra a da atividade 5 que ficará na forma y= 2x² - 2x – 4, também é importante pedir para a turma representar esta função graficamente no caderno para deixar registrado que os valores encontrados para x na resolução da fórmula canônica, são exatamente as abscissas dos pontos onde a função “intercepta” o eixo x.
A atividade a seguir pode assumir o papel de um desafio ou ainda uma avaliação.
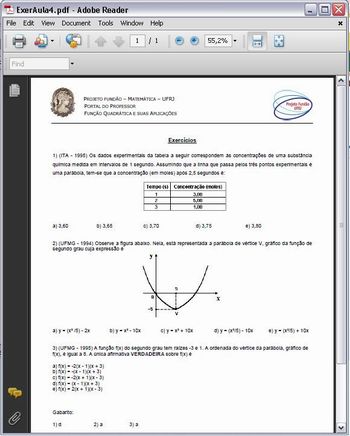
Professor, previamente acesse o link: http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/ExerAula4.pdf , tire cópias e distribua para os alunos que permanecerão em sala de aula.
Atividade 7:
Resolução e Correção de Exercícios
Peça aos alunos que se dirijam para a sala de aula, e distribua a atividade . Informe aos alunos que esta atividade tem como objetivos solidificar o conteúdo abordado trabalhado.
Figura 11: Imagem da autora
Permita a turma fazer descobertas e responder aos questionamentos. Peça aos alunos que relatem as suas descobertas e desenvolva no quadro de giz com a participação da todos as soluções encontradas.
Recursos Complementares
| Nome |
Tipo |
| Interação com Mathlets gerados pelo software Nippe Descartes |
Software Educacional |
| Interação com Simulações do Wolfram Demonstrations Project |
Simulações e Animações |
Página do Projeto Fundão: http://www.projetofundao.ufrj.br/matematica/
Para visualizar as atividades o professor deve:
1. Baixar o software Java disponível em: http://www.java.com/pt_BR/download/
2. Baixar o arquivo contendo as atividades.
Site consultado:
Veja também as seguintes aulas sobre este assunto:
- A Função Quadrática no Cotidiano (http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=24128)
- Cônicas no CAp UFRJ: Introdução (http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=12759)
- Cônicas no CAp UFRJ: Parábola (http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=12809)
- Equações do 2º grau no CAp UFRJ: Resolvendo via fatoração (http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=9517)
- Equações do 2º grau no CAp UFRJ: Resolvendo problemas (http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=9604)
- Resolução de equações do 2º grau no CAp UFRJ (http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=9573)
Avaliação
Tal avaliação deve ser feita ao observar as dúvidas dos alunos durante a realização das atividades sugeridas acima onde o professor terá a oportunidade de verificar o nível de entendimento ao circular pelos alunos durante a execução das atividades e também confirmar se o processo de construção do conhecimento foi concluído de maneira sólida através da correção, onde o professor perceberá como a turma se expressa sobre os conceitos.
Quatro estrelas 2 classificações
- Cinco estrelas 0/2 - 0%
- Quatro estrelas 2/2 - 100%
- Três estrelas 0/2 - 0%
- Duas estrelas 0/2 - 0%
- Uma estrela 0/2 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
ALDEIR JOSE MOURA DA SILVA, Universidade Potiguar , Rio Grande do Norte - disse:
aldeirj@hotmail.com14/12/2014
Quatro estrelasMuito bom!
-
dian, Unimontes , Minas Gerais - disse:
dianlucas01@hotmail.com14/10/2013
Quatro estrelaslegal
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus