08/02/2011
Rita Maria Cardoso Meirelles, Armando Tramontano, Edite Resende Vieira; Fernando Celso Villar Marinho, Jackson Lopes, Victor Paixão
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Tecnologia para a matemática |
| Ensino Médio | Matemática | Álgebra |
O que o aluno poderá aprender com esta aula
Utilizar inequações do segundo grau para resolver problemas do cotidiano.
Analisar o comportamento e desenvolver um processo para a resolução das inequações através do software Nippe Descartes.
Compreender, trabalhando o tema reciclagem de lixo, que a sociedade precisa de cidadãos conscientes para preservar e melhorar o ambiente onde vivem.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Função Afim
Função Quadrática
Intervalos Reais
Inequações do Primeiro Grau
Estratégias e recursos da aula
Professor, para realizar essa aula, encaminhe sua turma para o laboratório de informática e solicite aos alunos que se distribuam em, no máximo, três alunos por computador.
Atividade 1:
Materiais recicláveis
O objetivo desta atividade é facilitar a visualização dos retornos tanto econômicos quanto ecológicos, conseguidos com a reciclagem dos resíduos sólidos urbanos.
Nota: Antes de executar o aplicativo é necessária a sua instalação através do arquivo "verdes16". Para a sua execução utiliza-se o arquivo "VERDESpt"
Selecione o botão Assistir o vídeo de apresentação e com o auxílio do Data Show exiba a apresentação sobre a geração de lixo urbano que é, sem dúvida, um dos grandes problemas atuais e do futuro da humanidade.

Imagem da autora editada a partir de http://www.reciclaveis.com.br/suprim/verdes/
Simule junto com a turma várias situações e composições de resultados da reciclagem dos cinco principais produtos que compõem os "restos" da sociedade contemporânea, tais como: lata de alumínio, lata de aço, papel e papelão, plástico e vidro.
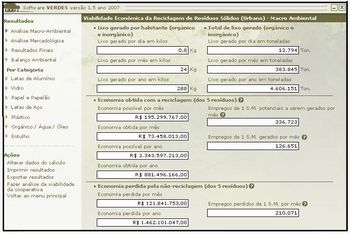
Imagem editada pela autora a partir de http://www.reciclaveis.com.br/suprim/verdes/
Atividade 2:
Inequações no dia-a-dia
A atividade a seguir trata de uma aplicação da inequação de segundo grau onde a turma atenderá de forma intuitiva às condições que satisfazem um exemplo do cotidiano.

Este exemplo, a definição e os questionamentos das outras atividades desta aula encontram-se disponíveis em http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/InequaAluno.pdf .
Portanto, previamente, imprima, faça cópias e distribua.
Reserve um tempo para a exploração da atividade.
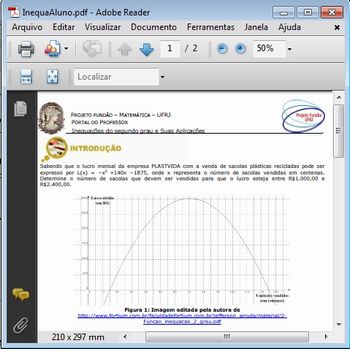
Imagem da autora
Após o término do tempo previsto, debata a solução com a turma a partir da análise gráfica.

O lucro da empresa Plastvida estará entre R$1.000,00 e R$ 2.400,00 quando o número de sacolas plásticas vendidas estiver entre 2500 e 4500 (25 e 45 centenas) ou quando o número de sacolas plásticas vendidas estiver entre 4500 e 9500 (45 e 95 centenas).
Atividade 3:
Definição de Inequação do Segundo Grau

Faça a construção junto com a turma.
Definindo inequações do segundo grau:
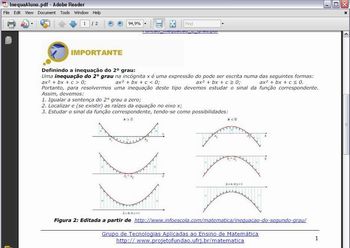
Imagem da autora
Peça aos alunos fazerem suas anotações no material recebido no início da aula que se encontra no link: http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/InequaAluno.pdf.

Atividade 4:
O objetivo é construir com a turma um método para resolver inequações, onde as funções quadráticas correspondentes possuem raízes reais.

Solicite aos alunos que acessem o link http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/Inequacoes1.html;
Solicite sugestões para resolvê-lo. Reserve um momento para o diálogo e troca de ideias.
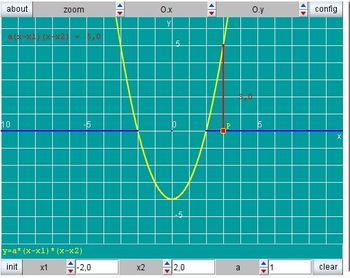
Imagem da autora
Verifique então as respostas dadas pela turma.
Nota: Registre no material dado que quando a função quadrática correspondente possui delta igual a zero ou maior que zero podemos representar a função na forma fatorada e determinar os valores de x que satisfazem as inequações dadas utilizando as raízes como referências.

a) i) a = 1, x1 = 1 e x2 = 1; ii) a = - 1; x1 = - 2 e x2 = 3; iii) a = - 5; x1 = - 1 e x2 = 1,6; iv) a = 2; x1 = 2 e x2 = 2.
b) Manipulação gráfica
c) Manipulação gráfica
d) i) A desigualdade é satisfeita para todos os valores de x reais que sejam diferentes de 1.
ii) A desigualdade é satisfeita para todos os valores de x reais que sejam maiores ou iguais a -2 ou menores ou iguais a 3.
iii) A desigualdade é satisfeita para todos os valores de x reais que sejam menores ou iguais a -1 ou maiores ou iguais a 1,6.
iv) Esta desigualdade não é satisfeita para os reais, isto é, a solução é vazia.
e) A parte azul corresponde aos valores de x para os quais a função é positiva e a parte branca onde é negativa.
O sinal de igual nas desigualdades corresponde aos valores de x que fazem com que y seja igual a zero, ou seja, são os zeros ou raízes da função.
f) Sim, este procedimento falha quando a função não possui raízes reais, pois a mesma não pode ser representada na forma fatorada.
Atividade 5:
O objetivo é resolver a inequação quando a função quadrática correspondente não possui raízes reais.

Solicite que os alunos acessem o link: http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/Inequacoes2.html
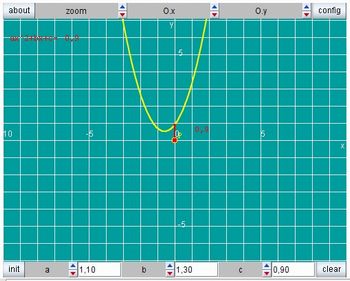
Imagem da autora
Deixe que eles a explorem por um tempo de aproximadamente 15 minutos.
Em seguida, questione sobre as descobertas feitas pela turma, verificando se os alunos apreenderam, com êxito, os conceitos trabalhados.

a) Leitura do problema
b) Manipulação gráfica
c) Manipulação gráfica
d) i) Todos os reais satisfazem esta desigualdade ii) Nenhum real satisfaz esta desigualdade
e) Não é possível pois f(x) não possui raízes reais.
f) i) g(x) > 0 Todos os reais satisfazem esta desigualdade
ii) g(x) < 0 Nenhum real satisfaz esta desigualdade
iii) h(x) > 0 Nenhum real satisfaz esta desigualdade
iv) h(x) < 0 Todos os reais satisfazem esta desigualdade
Atividade 6:
O objetivo é fazer com que o aluno perceba que a inequação pode ser apresentada utilizando-se funções diferentes da função nula nos dois membros da desigualdade.
Peça a turma que acesse o link: http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/Inequacoes3.html.
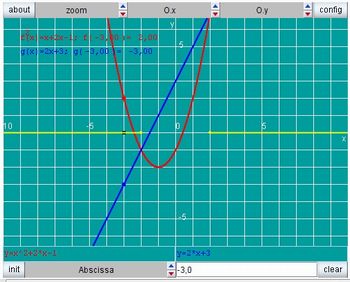
Imagem da autora
Estipule um tempo para que eles manipulem, façam descobertas e respondam aos questionamentos de acordo como perfil da sua turma.
Peça que os alunos relatem as suas descobertas e desenvolva no quadro com a participação da todos as soluções encontradas.

a) Análise gráfica
b) i) f ( - 4 ) > g ( - 4 ) ii) f ( - 1 ) < g ( - 1 ) iii) f ( 5 ) > g ( 5 )
c) Manipulação gráfica
d) Os trechos em amarelo correspondem aos valores de x onde f(x) > g(x).
e) Os valores de x qua satifazem a inequação são aqueles que são menores que -2 ou maiores que 2.
Atividade 7:
O objetivo é comparar as resoluções geométrica e algébrica de uma inequação.

Solicite a turma que resolva a desigualdade trabalhada na atividade 6 algébricamente, isto é, utilizando os princípios aditivo e multiplicativo.
Os alunos devem perceber que as soluções são iguais.

Para chegarmos à mesma solução algéricamente, devemos proceder como na inequação do primeiro. Daí:
x2 + 2x - 1 > 2x + 3 ,
x2 + 2x +(-2x) - 1 > 2x +(-2x) + 3,
x2 - 1 + (-3)> 3 + (-3),
x2 - 4 > 0
Agora, devemos resolver a equação x2 - 4 = 0, cujas soluções são x1 = - 2 e x2 = 2 e verificar quais os valores de x que são maiores que zero.
Para esta questão temos que os valores de x que satisfazem a inequação são aqueles que são menores que -2 ou maiores ou iguais a 2, ou seja, são estes valores que fazem parte do conjunto solução desta inequação.

A atividade a seguir pode ser utilizada como um desafio, ou mesmo, como avaliação.
Professor, previamente acesse o link http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/IneqSegGrauAluno.pdf e tire cópias do arquivo para serem distribuídas os alunos.
Atividade 8:
Outras Aplicações
Informe-os de que esta atividade tem como objetivos solidificar o conteúdo trabalhado, além de mostrar como as inequações do segundo grau são utilizadas em diferentes situações do cotidiano.

Imagem da autora
A resolução das questões encontra-se no link http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/IneqSegGrauProfessor.pdf.
Permita que eles façam descobertas e respondam aos questionamentos.
Peça aos alunos que relatem o encaminhamento de suas resoluções e desenvolva no quadro de giz, com a participação de todos, as soluções encontradas.

Apresente com o auxílio do Data Show:
1. A reportagem especial Sacolas pláticas que mostrar alternativas de reciclagem e utilização mais adequada das mesmas.

Imagem da autora editada a partir de http://www2.camara.gov.br/tv/materias/CAMARA-INFORMA/187370-SACOLAS-PLASTICAS.html
Para tanto, acesse o link: http://portaldoprofessor.mec.gov.br/fichaTecnica.html?id=28532.
2. O áudio que permitir que o aluno ampliar seus conhecimentos sobre a reciclagem e seus benefícios, e entender a importância econômica e ambiental desse processo utilizando a coleta seletiva.
Para tanto, acesse o link: http://portaldoprofessor.mec.gov.br/fichaTecnica.html?id=31181.
Promova um debate sobre este tema e finalize sua aula convidando a turma a organizar a coleta seletiva em sala de aula.
Recursos Educacionais
| Nome | Tipo |
|---|---|
| VERDES - Viabilidade Econômica de Reciclagem dos Resíduos Sólidos | Software Educacional |
Recursos Complementares
Fontes de Pesquisa
1. Software Nippe Descartes
O grupo de pesquisa “Tecnologias no Ensino da Matemática”, vinculado ao Projeto Fundão, confeccionou diversas atividades utilizando o software Nippe Descartes, um aplicativo desenvolvido em Java que permite uma manipulação ágil e simples de janelas gráficas aplicáveis a qualquer página web. Este grupo reúne-se semanalmente e se propõe a desenvolver aplicações específicas para apresentação de conteúdos do Ensino Médio.
Página do Projeto Fundão: http://www.projetofundao.ufrj.br/matematica/
Para visualizar as atividades o professor deve:
a) Baixar o software Java disponível em: http://www.java.com/pt_BR/download/
b) Baixar o arquivo contendo as atividades.
2. Veja também as aulas que complementam este assunto:
- A Geometria na Construção do Conceito de Função Linear
- Telefonia Celular: Qual operadora escolher? Um Problema para ser Resolvido com a Função Afim
- Procurando uma Estratégia para não Sair no Prejuízo: Estudo de Inequações do 1º grau
- Função Quadrática e suas Aplicações
- A Função Quadrática no Cotidiano
Avaliação
Tal avaliação deve ser feita ao observar as dúvidas dos alunos durante a realização das atividades sugeridas na atividade 8.
Quatro estrelas 1 classificações
- Cinco estrelas 0/1 - 0%
- Quatro estrelas 1/1 - 100%
- Três estrelas 0/1 - 0%
- Duas estrelas 0/1 - 0%
- Uma estrela 0/1 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
leirivanio, EEFM Irmão urbano gonzalez , Ceará - disse:
leirivanio@yahoo.com.br14/05/2011
Quatro estrelasAula muito boa bastante ilustrativa e aplicada.
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus




