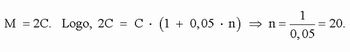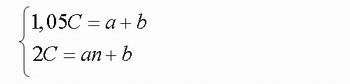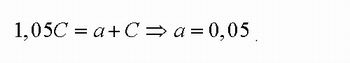Identificar a função polinomial do 1º grau em situações de juros simples;

Criar e resolver problemas contextualizados em situações de juros simples a partir de gráficos de funções polinomiais do 1º grau.

Leitura, interpretação e confecção de gráficos de função afim.

2 aulas de 50 minutos cada

Frações e Porcentagem.

Notação decimal.

Juros simples.

Progressão aritmética.

Função afim.

Reconhecimento de taxas.

Períodos de aplicação.

Como relacionar os juros simples a funções polinomiais do 1º grau? Um caminho possível é relacioná-los a partir das progressões aritméticas. Espera-se que as três atividades propostas nesta aula levem os alunos a estabelecer esta correspondência.     

Inicie a aula com um exemplo simples que possibilite "enxergar" algumas regularidades no cálculo dos juros e no gráfico gerado pelos valores obtidos.

Atividade 1 

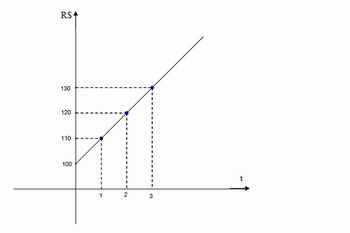
Calcular o montante no n-ésimo mês de uma aplicação de R$ 100,00 à taxa de 10% a.m. a juros simples.

Professor, essa atividade tem por objetivo estabelecer uma correspondência entre a representação utilizada comumente na resolução de problemas de matemática financeira e a utilizada para funções e para progressões aritméticas. Caso julgue necessário, faça um exercício básico de revisão de PA se os alunos apresentarem dificuldades ao recordar elementos como primeiro termo, termo geral, razão, etc.

Apresente o problema acima e dê um tempo para os alunos resolverem.

Em seguida apresente a solução indicada abaixo, bem como o comentário "importante" em destaque.

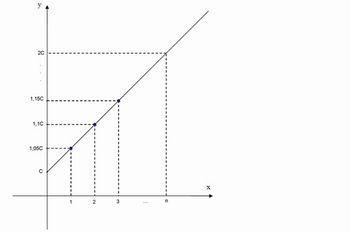
Observe que os montantes obtidos formam uma Progressão Aritmética (P. A.) com primeiro termo M₀ e razão M₀ . i. O gráfico que dá esses valores em função do tempo é representado por pontos colineares e, portanto, está contido no gráfico de uma função polinomial do primeiro grau ou função afim.

Mostrar para os alunos a diferença de notação utilizada na representação do montante em função do tempo ajudará na compreensão da relação entre juros simples e função do 1º grau.

A expressão M_n=100+10n indica o valor do montante no tempo n.

Se o tempo for representado pela letra x teríamos M_x=100+10x

Além disso, a representação da imagem de x pela função M costuma ser representada por M(x).

Ficaríamos com M(x) =100+10x

Por fim, costuma-se utilizar a letra f para representar a função, neste caso, trocando M por f teríamos:

f(x) =100+10x

Essas transformações são muito úteis para que os alunos estabeleçam corretamente a correspondência entre os conceitos matemáticos envolvidos. A diferença nas representações pode significar um grande obstáculo epistemológico.

Nota: É importante que os alunos percebam a possibilidade de se resolver problemas tanto com o raciocínio de juros simples, como por P.A. ou por função afim.

Atividade 2

Essa atividade irá estimular a criatividade dos alunos e os auxiliará a estabelecer a correspondência entre os conceitos relativos a funções, PA e juros simples.

1º) Divida a turma em grupos com no máximo quatro alunos.

2º) Cada grupo deverá escrever em uma folha de papel (avulsa), quatro funções do 1º grau.

3º) Em seguida os grupos devem trocar entre si as funções e a partir delas enunciar (e registrar em uma outra folha) quatro problemas de matemática financeira, envolvendo juros simples, que sejam modelados pelas funções indicadas.

Por exemplo, se foi escrita a função f(x)=20x+100, o aluno poderá observar que:

O valor inicial é 100, porque f(0)=0+100=100. Além disso, após o período de uma unidade de tempo, o valor acumulado será

f(1)=20+100=120.

Daí é possível obter o valor dos juros correspondentes a uma unidade de tempo: 120-100=20

E a taxa de juros que será igual a 20/100=20%.

Neste caso, um problema possível seria:

Um capital de R$100 reais foi aplicado, em regime de juros simples, a uma taxa de 20% ao mês. Qual o montante correspondente a aplicação deste capital em função do tempo (em meses)?

4º) Ao término deste momento, recolha as folhas com os enunciados e redistribua as folhas com as funções de modo que um grupo sempre pegue a folha de outro.

5º) Agora, leia o enunciado dos problemas e peça para os grupos identificarem qual deles tem as funções correspondentes.

6º) Assim que um grupo tiver identificado o par problemas/funções, peça para que eles leiam todos os problemas para turma e mostrem as funções utilizadas. Neste momento, todos devem estar muito atentos para identificar possíveis erros. Essa atividade irá auxiliar na fixação deste conceito.

Atividade 3

Professor, acesse a página com o construtor de gráficos a seguir  

http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/FuncaoAfim.html

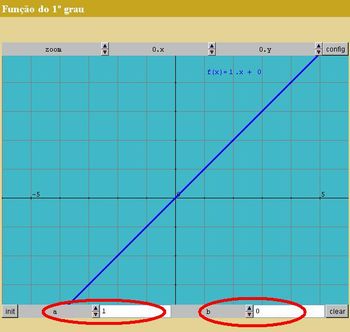
e mostre aos alunos como modificar os valores dos parâmetros a e b em destaque na figura abaixo. Cada modificação irá gerar um gráfico diferente.

Em seguida peça para os alunos escreverem a função afim correspondente a cada indicação dada abaixo.

f(x)= 25x+350

f(x)= 30x+100

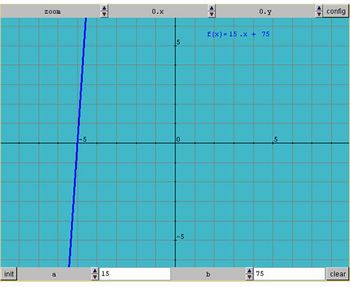
f(x)= 15x+75

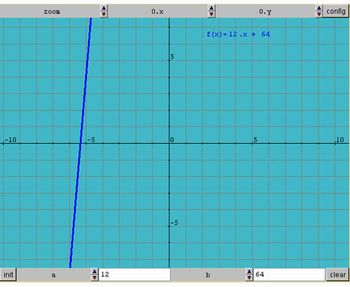
f(x)= 12x+64

Depois peça para eles criarem um problema de juros simples que seja modelado por estas funções.

Escolha, ao acaso, um aluno e peça para ele ler um dos problemas propostos. Os outros alunos deverão indicar qual dos gráficos foi utilizado como modelo para a criação do problema. Repita este processo até finalizar todos os gráficos propostos.

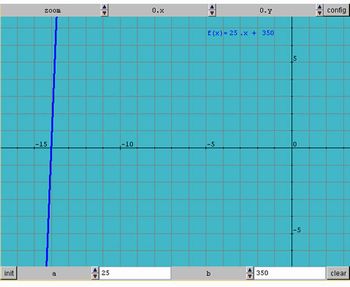
f(x)= 25x+350

 

Imagem retirada do link: http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/FuncaoAfim.html 

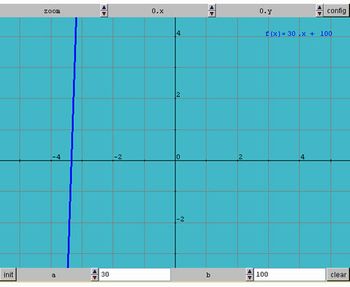
f(x)= 30x+100

Imagem retirada do link: http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/FuncaoAfim.html

f(x)= 15x+75

Imagem retirada do link: http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/FuncaoAfim.html

f(x)= 12x+64

Imagem retirada do link: http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/FuncaoAfim.html

Atividade 4

Peça para os alunos utilizarem o conceito de função afim ou de juros simples para resolver esta atividade. O ideal é convidar até três alunos para apresentarem suas soluções caso estas sejam distintas.

Um capital é aplicado em regime de juros simples, à uma taxa mensal de 5%. Depois de quanto tempo este capital estará duplicado?

Solução por Juros Simples:

Sendo C o capital, temos

Portanto, este capital estará duplicado após um período de 20 meses.

Solução por função afim:

Como a função é do 1ª grau, temos f(x) = ax + b, e escrevendo a lei de formação da função teremos o seguinte sistema:

Como o gráfico da função intersecta o eixo y em C, temos que b = C e, portanto,

Logo, o sistema fica assim reescrito:

Abaixo seguem algumas atividades que podem ser trabalhadas com os alunos para fixar o conteúdo estudado:

1. Se Paulo investiu R$ 5 500,00, à taxa de juros simples de 12% ao mês, qual será o montante se o capital ficou aplicado por 6 meses?
2. Calcule a taxa de aplicação para um capital de R$ 1 500,00 aplicado a juros simples, durante 6 meses, que gerou um montante de R$ 1 680,00.

Fonte: NASSER, Lilian. Matemática financeira para a escola básica: Uma abordagem prática e visual – UFRJ/IM – Projeto Fundão   

http://www.projetofundao.ufrj.br/matematica/images/stories/matfin.jpg  

1. Temos C = 5 500,00; i = 12% a.m; n = 6 meses.

M=C(1+ni)=5500(1+6x0,12)=5500+5500x0,72=9460.

Solução por função afim:

Temos o sistema com equações {1,12C = a + b  e  M = a6 + b} Como o gráfico da função intersecta o eixo y em C, temos que b = C e, portanto, Utilizando a primeira equação temos, 1,12 x 5 500 = a + 5 500 Assim a = 660 Agora utilizando a segunda equação temos, M = 660 x 6 + 5 500 = 9 460,00

2. Temos n = 6 meses, C = 1 500,00 ; M = 1 680,00.

M=C(1+ni)

1680=1500(1+6i)=1500+9000i

i=180/9000=0,02=2%

Solução por função afim:

Temos o sistema com equações {(1 + i)C = a + b  e  M = an + b}

Como o gráfico da função intersecta o eixo y em C, temos que b = C e, portanto,

Utilizando a segunda equação temos, 1 680 = a6 + 1 500

Assim a = 30

Agora utilizando a primeira equação temos, (1 + i) x 1 500 = 30 + 1 500

Assim i =  0,02, e portanto 2% ao mês.

Acesso aos links:  

http://www.projetofundao.ufrj.br/matematica/index.php?option=com_content&task=view&id=6&Itemid=18 

Aulas do Portal

• Matemática Financeira no CAp UFRJ: Introdução 

http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=9918 

• Matemática Financeira no CAp UFRJ: Juros Compostos 

http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=9932 

• Matemática Financeira no CAp UFRJ: Equivalência de Capitais 

http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=9935 

• Matemática Financeira no CAp UFRJ: Equivalência de Taxas 

http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=9939 

• Matemática Financeira no CAp UFRJ: Cálculo de Prestações 

http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=10063 

• Matemática Financeira no CAp UFRJ: Cálculo de Taxa de Juros 

http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=10069 

• Matemática Financeira no CAp UFRJ: Opções de Pagamento 

http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=12978 

• Matemática Financeira no CAp UFRJ: Opções de Pagamento e o Excel 

http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=13004 

• Matemática Financeira no CAp UFRJ: Sistemas de Amortização 

http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=12982 

• Matemática Financeira no CAp UFRJ: Tabela Price e o Planilhas Eletrônicas 

http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=12989 

• Matemática Financeira no CAp UFRJ: SAC e o Planilhas Eletrônicas 

http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=12991 

A avaliação deve ser feita ao longo de toda a aula baseada na participação dos alunos nas atividades propostas. É importante certificar-se de que eles tenham compreendido a associação entre os juros simples e a função polinomial do primeiro grau. Não queremos que essa associação vire uma simples repetição de fórmulas! Neste caso, recomendamos que as atividades 3 e 4 sejam utilizadas como avaliações em grupos. Isso poderá aumentar o empenho dos alunos na resolução destas atividades. Dê sempre um bônus pela criatividade dos alunos na criação de problemas interessantes, que sejam diferentes dos exemplos dados!