18/09/2009
Marco G. B. Burlamaqui
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Números e operações |
| Ensino Médio | Matemática | Geometria |
| Ensino Médio | Matemática | Álgebra |
O que o aluno poderá aprender com esta aula
• Situações da vida real
• Interpretar o comportamento das funções periódicas com as demais áreas do conhecimento.
• Construir conceitos de amplitude (máximos e mínimos de uma função), período e frequência;
• Interpretar e fazer uso de modelos para a resolução de problemas trigonométricos;
• Despertar o interesse do aluno e auxiliar na resolução de problemas envolvendo funções periódicas;
• Saber ler, interpretar e mostrar a construção de gráficos relacionados ao movimento periódico e identificar as alterações;
• Construir conceitos de amplitude (máximos e mínimos de uma função), período e frequência.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
• Unidade de medidas de ângulos: Graus e Radianos (http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=1477)
• Medir ângulos (http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=3768)
• Círculo trigonométrico:
o http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=1203
o http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=770
• Definição de seno, cosseno e tangente em um triângulo retângulo.
Estratégias e recursos da aula
Primeira aula
Olá Professor, vamos apresentar uma forma diferente de apresentar o assunto “Gráfico de funções trigonométricas” aos nossos alunos. É importante comentar aos seus alunos que muitos fenômenos físicos e sociais de comportamento cíclico, ou periódico, podem ser modelados por funções trigonométricas. Daí a enorme aplicação desse estudo em campos variados da ciência, como Acústica, Astronomia, Economia ou Medicina. Uma circunstância exemplar é o monitoramento da frequência cardíaca, isto é, do número de batimentos cardíacos em um período de tempo, geralmente medido em bpm (batimentos cardíacos por minutos). Apresente a eles uma situação para eles possam refletir sobre o assunto, como exemplo:
No gráfico abaixo, a variação da pressão sanguínea P (em mmHg) de certo indivíduo, em função do tempo, em segundos, é uma função cíclica, sendo que cada ciclo completo (período) equivale a um batimento cardíaco.
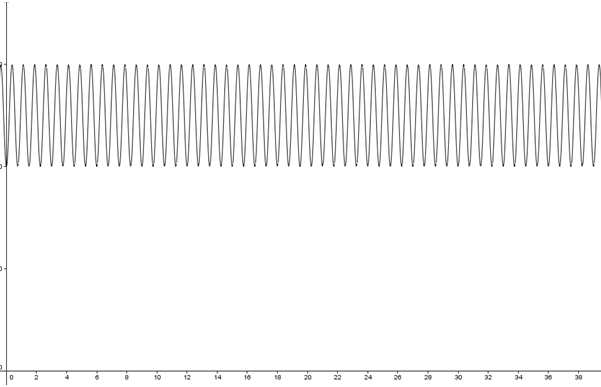
Sabe-se que o gráfico representa a função periódica cuja a lei de formação é P(x)=100-20.cos(8π/3.x), em que o valor do argumento (8π/3.x) é dado em radiano. (Onde π é a letra grega pi).
a) Aplicando essa lei, determine P quando t = 2s.
b) Aplicando essa lei, determine o menor valor de x para P=100 mmHg. Verifique a resposta no gráfico.
Peça aos seus alunos que acessem o sítio http://ecalculo.if.usp.br/funcoes/trigonometricas/ftrigonometricas.htm e façam uma leitura do texto sobre o assunto.
Para começar as atividade de consolidação do conhecimento, peça a eles que acessem o sítio http://objetoseducacionais2.mec.gov.br/bitstream/handle/mec/5990/SpinningOutSineAndCosine.nbp?sequence=1, trata-se de uma pequena aplicação que mostrará a eles que uma primeira visão do gráfico das funções trigonométricas.
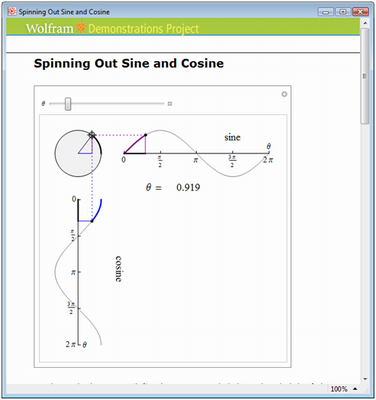
Professor, o aplicativo anterior nos mostra que construímos os gráficos das funções trigonométricas com o auxílio da tabela, com valores de x da 1ª volta positiva. Geralmente perdemos muito tempo calculando os valores das funções:
* Seno ==> http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=771
* Cosseno ==> http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=772
* Tangente ==> http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=773
e também com o auxílio do ciclo trigonométrico, disponível em http://www.professores.uff.br/hjbortol/geogebra/activities/2007.2/funcoes-trigonometricas.html. (Veja também em http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=1203 e http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=770).
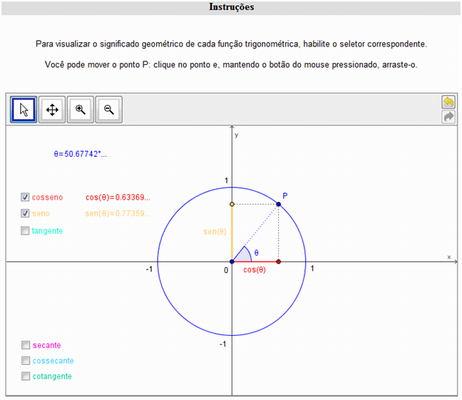
Quando abordamos o assunto “Gráfico de funções trigonométricas” temos que comentar determinados aspectos:
* Construção do gráfico
* Tipos de gráficos: inicialmente o gráfico f ( x ) = a * sen (b + c*x) e g ( x ) = a * cos (b + c*x) onde a, b e c são constantes arbitrárias. Estes tipos podem ser subdivididos em:
** y = c + senx ou y = c + cos x ou y = c + tg x
** y = sen(x + b) ou y = cos(x + b) ou y = tg(x + b)
** y = d . sen(x) ou y = d . cos(x) ou y = d . tg(x)
** y = sen(d.x) ou y = cos(d.x) ou y = tg(d.x)
* Periodicidade da função
* Sinal da função
* Variação da função
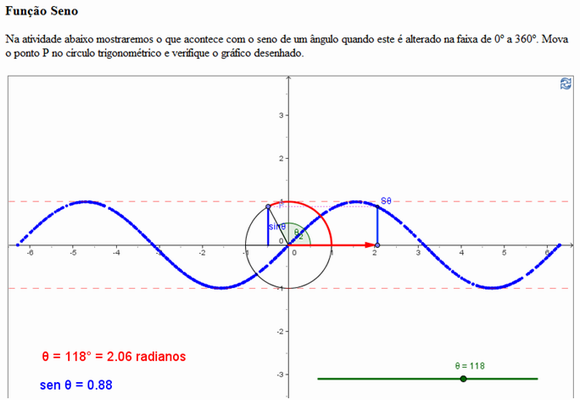
Professor, peça aos seus alunos que acessem o sítio http://www.dmm.im.ufrj.br/projeto/rived/modulo_trigonometria/index.htm trata-se de um aplicativo que vai trabalhar com a construção de gráficos.

Na parte de baixo da tela tem as setas de comando de mudança de página e atividades

clique na seta da direita para c ontinuar. Será apresentad a a tela da função seno, cosseno e tangente. Para movimentar o ponto P, basta clicar no ponto da linha verde e deslizar na horizontal. Para ter acesso as outras funções, basta deslocar para a parte de baixo da tela.
Segunda aula
Professor, para que os alunos possam fazer a análise dos diversos tipos de funções trigonométricas, utilizaremos o GeoGebra, para consolidar os conhecimentos teóricos vistos nos links anteriores. Vamos realizar uma atividade no laboratório de informática utilizando um software de geometria dinâmica, http://www.geometriadinamica.com/, o GeoGebra. Ele é para se utilizar em ambiente de sala de aula. Ele reúne GEOmetria, álGEBRA e cálculo. Esta disponível em http://www.geogebra.org/ em versão para download gratuito ou para ser executado via web (WebStart).
No caso desta atividade, tenha instalado previamente o GeoGebra em todos os computadores do laboratório de informática. Como documentação do software, temos:
* O manual disponível em http://www.geogebra.org/h elp/docupt_BR.pdf e outro http://www.geogebra.org/help/docupt_PT.pdf, este em português de Portugal, mas um pouco mais completo;
* Uma apostila sobre a utilização esta disponível em http://www.tinaeducacao.com.br/wp-content/uploads/2008/11/apostilageogebra_2007.pdf, nesta apostila temos várias atividades utilizando o software, e
* Um guia rápido de comandos, disponível em http://cattai.mat.br/site/files/geogebra/guia_rapido_geogebra.pdf.
Professor, vamos mostrar aos alunos maneiras de proceder para construção de gráficos de funções. Peça a eles que sigam os seguintes passos.
Passo 1: Inicie o aplicativo GeoGebra, aparecerá a seguinte tela:
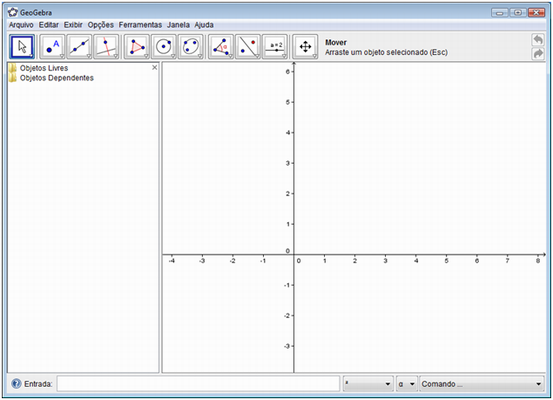
Professor, comente com seus alunos que na barra de botões,

temos diversas ferramentas que podem ser utilizadas. Em todos os botões aparece uma seta no canto inferior direito, que, ao ser clicada, permite visualizar as opções existentes.

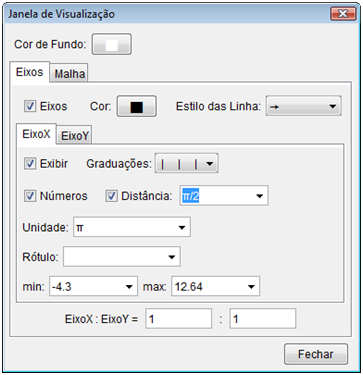
Passo 2: Exibir malhas. No menu “Exibir”, selecione a opção “Malha”.
Passo 3: Trocar as unidades de medid as o eixo x para radianos. Na área de trabalho, clique com o mouse com bot ão da direita e será mostr ada o menu “Janela de Visualização” e será mostrada a seguinte tela de configuração. No combo “Unidades”, selecione a opção “π” (letra grega pi). Em seguida, marque o chebox “Distância” e no seu combo, selecione a opção “π/2”, con forme tela abaixo.
Professor, vamos iniciar o trabalho de análise com a função seno.
Passo 4: Criar o gráfico da função. Na parte de baixo do aplicativo, existe uma caixa de texto destinada a entrada de dados e de fórmulas,

Digite: f(x)=sin(x).
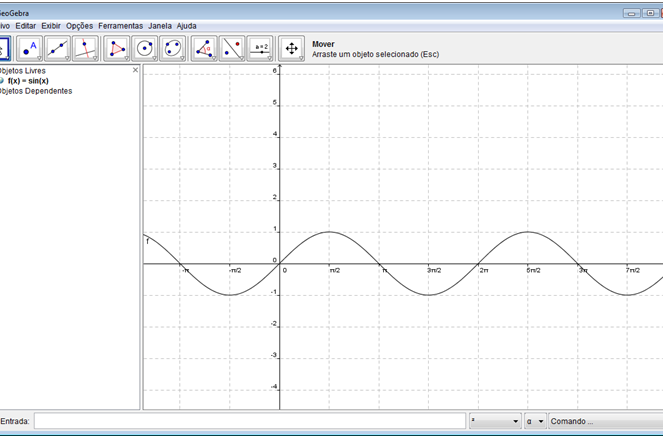
Professor, observe que no lado esquerdo da tela aparece uma lista de objetos dependentes. Neste caso temos um objeto livre. Podemos alterar este objeto, basta dar dois cliques com o mouse em cima do objeto e alterá-lo, ou, dar um clique com o botão da direita do mouse e será mostrado o menu “Função f” e selecione a opção propriedades. Será mostrada a seguinte tela de configuração onde se pode alterar a definição da função, bem com outras características, como cor, espessura e estilo da linha do gráfico, dentre outras.
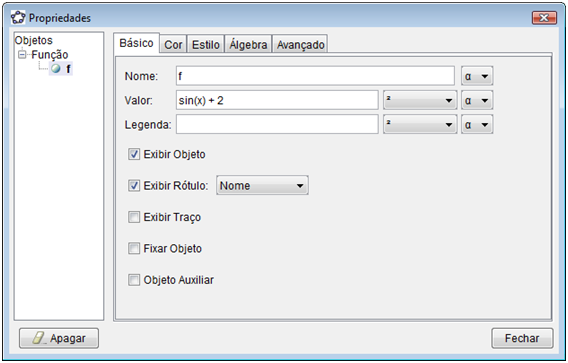
Alterando para f(x)=sin(x) + 2, teremos o gráfico na tela mostrado na tela abaixo. Depois de mostra aos alunos esta possibilidade, comente com os alunos que podemos montar qualquer tipo de gráfico, bem com das outras funções trigonométricas, com secante, cossecante e cotangente.
* Tipos de gráficos: inicialmente o gráfico f ( x ) = a * sen (b + c*x) e g ( x ) = a * cos (b + c*x) onde a, b e c são constantes arbitrárias. Estes tipos podem ser subdivididos em:
** y = c + senx ou y = c + cos x ou y = c + tg x
** y = sen(x + b) ou y = cos(x + b) ou y = tg(x + b)
** y = d . sen(x) ou y = d . cos(x) ou y = d . tg(x)
** y = sen(d.x) ou y = cos(d.x) ou y = tg(d.x)
Peça a eles que crie um novo gráfico, como exemplo, g(x) = cos(x). Altera as propriedades de cor para uma melhor visualização. Experimente criar uma função h(x)=tan(x) e uma i(x)=sin(x)/cos(x) e pergunte a eles o que aconteceu. Por quê? Para apagar o gráfico das funções criadas, basta clicar com o mouse no objeto e em seguida pressione a tecla “Delete”.
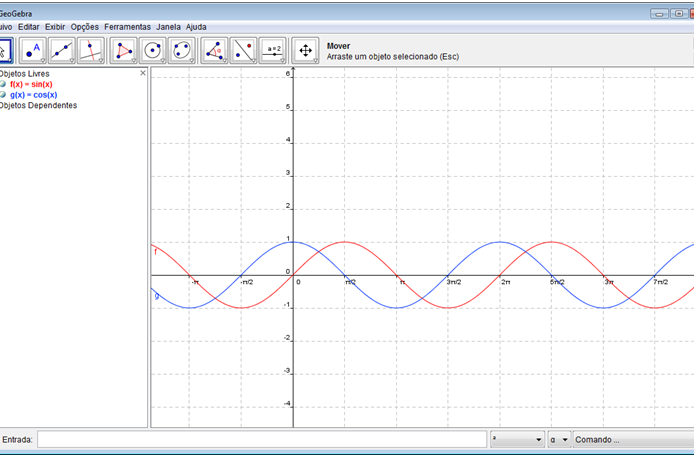
Professor, aproveite este momento para dar um tempo aos alunos para que e les exp erimentem a criação dos diversos tipos de gráficos f ( x ) = a * sen (b + c*x) e g ( x ) = a * cos (b + c*x) onde a, b e c são constantes arbitrárias . Após o tempo, faça o s seguintes questionamentos:
* O que acontece quando aumentamo s os valores de “c”? E quando diminuímos?
* E com os valores de “c”?
* E com os valores de “a”?
* Dentro de qual intervalo os valores de f(x) começa a se repetir? Qual é o nome dado a este intervalo.
* O intervalo do maior e o menor valor que f(x) pode assumir é chamado de amplitude da função. Qual é o conjunto relacionado à amplitude?
* Quais são os intervalos de x em que os valores de f(x) são positivos? E negativos? E iguais a zero?
Eles devem observar que:
* Quando alteramos o valor de “a”, com relação à operação de soma, o gráfico sofre uma translação de |a| unidades, no eixo y, em relação ao gráfico original, da seguinte forma:
** Se a>0, a translação é para cima;
** Se a<0, a translação é para baixo.
* Quando alteramos o valor de “a”, com relação à operação de multiplicação, o gráfico sofre uma alteração na sua amplitude.
* Quando alteramos o valor de “b” o gráfico sofre uma translação de |b| unidades, no eixo x, em relação ao gráfico original, da seguinte forma:
** Se b>0, a translação é para a esquerda;
** Se b<0, a translação é para a direita.
* Quando alteramos o valor de “c” o gráfico sofre uma alteração no período em relação ao gráfico original, da seguinte forma:
** Se c>0, o período diminui;
** Se c<0, o período aumenta.
* O intervalo em que os intervalos se repetem chama-se período.
* O conjunto relacionado à amplitude é o conjunto imagem da função.
Peça aos alunos que retornem a função f(x)=sin(x). Vamos mo strar de uma maneira mais concreta os pontos:
* Sinal da função
* Variação da função
* Conjunto imagem
Passo 5: Criar um seletor. No décimo botão da barra de botões, selecione a ferramenta “Seletor” e clique em um local na área de trabalho. Será mostrada a janela de propriedades do seletor. Selecione a opção “Ângulos” e em seguida clique em “Aplicar”. Note que para o seletor foi definida a letra grega “α” (alfa).

Passo 6: Criar um ponto dependente. No segundo botão da barra de botões, selecione a ferramenta “Novo ponto” e clique na intersecção dos eixos x e y. Existe outra forma de criar o ponto A. Na parte de baixo do aplicativo, existe uma caixa de texto destinada a entrada de dados e de fórmulas, "Passo 4". Bastaria digitar: A =(0,0). Mas o ponto que iremos criar será dependente do ângulo definido no seletor. Digite: A=(α,f(α)). Para digitar o símbolo “α”, recorra ao segundo combo na linha de entrada de dados. Para alterar o valor de “α”, clique e segure o mouse no ponto indicado no seletor e o movimente na horizontal.
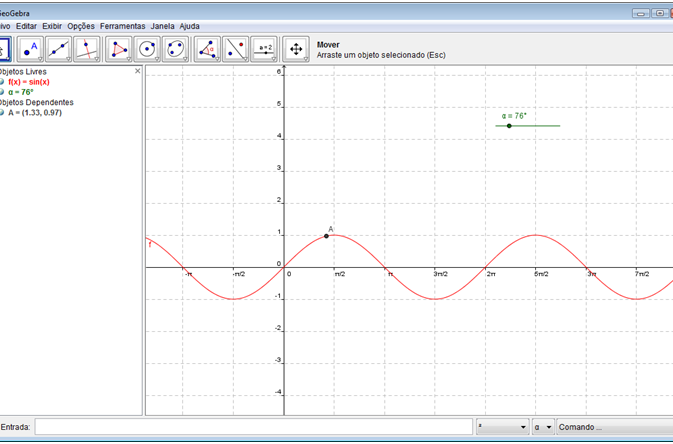
Peça aos alunos que observem os valores da abscissa e da ordenada do ponto A localizado na tela de objetos dependentes.
Professor, questione:
* Qual é o intervalo em que a função apresenta valores de f(x) crescentes? E decrescentes? A quais quadrantes estes intervalos correspondem?
* Qual é o intervalo que representa o período da função? Ou quando os valores de f(x) começam a repetir?
Vamos analisar a amplitude da função, ou seja, o conjunto imagem da função.
Passo 7: Criar um ponto dependente. Digite: B=(0,f(α)). Lembre-se que o conjunto imagem é aferido o eixo y, onde o valor da abscissa é zero. Clique e segure o mouse no ponto indicado no seletor e o movimente na horizontal. Professor, caso queira destacar bem o intervalo da imagem, selecione o ponto B o botão direito do mouse e marque a opção “Habilitar Rastro”, clique e segure o mouse no ponto indicado no seletor e o movimente na horizontal.
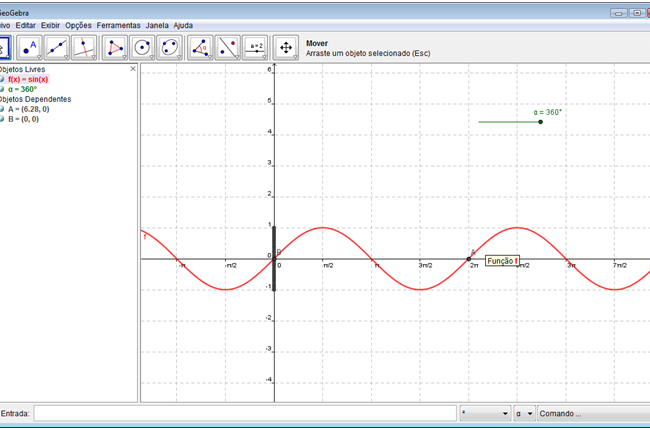
Professor, peça aos alunos para identificar o intervalo correspondente ao conjunto imagem. Em seguida, altere o valor da função f(x) e analise os aspectos comentados na aula.
Professor elabore uma lis ta de exercícios para que seu s alunos possam trabalhar e consolidar os conhecimen tos adquiridos . Utilize o livro didático e caso se já necessário elabore uma lista de exercícios complementares , um exemplo esta dispo nível em http://www.ccmn.ufrj.br/curso/trabalhos/PDF/matematica-trabalhos/conceitos_tecnologias_funcoes/FJL.pdf , na página 4 e 5.
Recursos Complementares
Aulas do portal sobre o assunto
• http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=1621
Blogs e sites sobre o assunto
• http://educacao.uol.com.br/matematica/ult1705u45.jhtm
• http://trigono.vilabol.uol.com.br/conteudo.htm#%C3%82ngulos%20e%20Arcos%20Trigonom%C3%A9tricos
• http://liegednamanda.blogspot.com/2009/06/historia-da-trigonometria.html
Outros objetos de aprendizagem
• http://www.cienciamao.if.usp.br/dados/tex/_funcaotrigonometricasgraficosii.flash.swf
Avaliação
A avaliação, 1 aula, poderá ser da seguinte forma:
• Atividades em sala.
• Listas de exercícios envolvendo aplicações do assunto no cotidiano.
• Durante as aulas observando o interesse e a participação do aluno.
• Estimular os alunos a criarem e participarem de Blogs sobre o assunto. Caso queira utilizar algum Blog já existente, sugerimos os seguintes:
o http://liegednamanda.blogspot.com/2009/06/graficos-das-funcoes-trigonometricas-e.html
• Competição entre grupos, de no máximo quatro alunos, onde cada grupo apresenta um problema outro grupo caso consiga resolvê-lo, continua na competição, caso erre, será eliminado.
• Professor experimente criar um ambiente virtual onde você e os professores poderão criar blogs, webquest, fóruns, exercícios virtuais. Acesse http://www4.escola24h.com.br/.
Quatro estrelas 5 classificações
- Cinco estrelas 4/5 - 80%
- Quatro estrelas 1/5 - 20%
- Três estrelas 0/5 - 0%
- Duas estrelas 0/5 - 0%
- Uma estrela 0/5 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Dário, estudante , Paraná - disse:
dario_saraiva_br@hotmail.com16/12/2012
Cinco estrelasMUITO INTERESSANTE. COM ESTE SOFTWARE A AULA FICA ÓTIMA PARA APRENDER.
-
jairo, ufrn , Rio Grande do Norte - disse:
jairogta_007@hotmail.com22/08/2012
Cinco estrelasshow de bola
-
cirllainy, ribeiro caminha , Alagoas - disse:
cirllainy-carinhosa@hotmail.com29/09/2010
Cinco estrelastirei algumas duvidas e amei essa aula
-
Fabio Pires, uesb , Bahia - disse:
fabyopyres@hotmail.com14/09/2010
Cinco estrelasexcelente trabalhar a trigonometria utilizando o geogebra.
-
Jurema, E.E Irene Branco da Silva , São Paulo - disse:
eusougatoedai@yahoo.com.br04/08/2010
Quatro estrelasMuito interessante
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus


